题目内容
已知抛物线y2=4x.
(1)若圆心在抛物线y2=4x上的动圆,大小随位置而变化,但总是与直线x+1=0相切,求所有的圆都经过的定点坐标;
(2)抛物线y2=4x的焦点为F,若过F点的直线与抛物线相交于M,N两点,若
=-4
,求直线MN的斜率;
(3)若过F点且相互垂直的两条直线l1,l2,抛物线与l1交于点P1,P2,与l2交于点Q1,Q2.证明:无论如何取直线l1,l2,都有
+
为一常数.
(1)若圆心在抛物线y2=4x上的动圆,大小随位置而变化,但总是与直线x+1=0相切,求所有的圆都经过的定点坐标;
(2)抛物线y2=4x的焦点为F,若过F点的直线与抛物线相交于M,N两点,若
| FM |
| FN |
(3)若过F点且相互垂直的两条直线l1,l2,抛物线与l1交于点P1,P2,与l2交于点Q1,Q2.证明:无论如何取直线l1,l2,都有
| 1 |
| |P1P2| |
| 1 |
| |Q1Q2| |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)本题考查抛物线的定义,由于直线x+1=0是已知抛物线的准线,而圆心在抛物线上的圆既然与准线相切,则它必定过抛物线的焦点,所以所有的圆必过抛物线的焦点,即定点(1,0);
(2)设直线MN方程为y=k(x-1),把它与抛物线方程联立方程组,消去x,就可得到关于y的方程,可得y1+y2,y1y2,利用条件
=-4
,即可得出结论;
(3)过F点的直线l1为x=ky+1,代入抛物线方程,分别求出|P1P2|,|Q1Q2|,即可证明.
(2)设直线MN方程为y=k(x-1),把它与抛物线方程联立方程组,消去x,就可得到关于y的方程,可得y1+y2,y1y2,利用条件
| FM |
| FN |
(3)过F点的直线l1为x=ky+1,代入抛物线方程,分别求出|P1P2|,|Q1Q2|,即可证明.
解答:
(1)解:由题意,直线x+1=0是已知抛物线的准线,圆心在抛物线上的圆.
∵圆与准线相切,
∴圆必定过抛物线的焦点,
∴所有的圆必过抛物线的焦点,即定点(1,0);
(2)解:设M(x1,y1),N(x2,y2),则
设直线MN方程为y=k(x-1),把它与抛物线方程联立方程组,消去x,得y2-
-4=0
∴y1+y2=
,y1y2=-4,
∵
=-4
,
∴y1=-4y2,
∴k=±
;
(3)证明:设Q1(x3,y3),Q2(x4,y4),过F点的直线l1为x=ky+1,代入抛物线方程得y2-4ky-2=0,
∴y3+y4=4k,y3y4=-2,
∴|P1P2|=x3+x4+2=k(y3+y4)+4=4k2+4,
同理|Q1Q2|=
+4,
∴
+
=
为一常数.
∵圆与准线相切,
∴圆必定过抛物线的焦点,
∴所有的圆必过抛物线的焦点,即定点(1,0);
(2)解:设M(x1,y1),N(x2,y2),则
设直线MN方程为y=k(x-1),把它与抛物线方程联立方程组,消去x,得y2-
| 4y |
| k |
∴y1+y2=
| 4 |
| k |
∵
| FM |
| FN |
∴y1=-4y2,
∴k=±
| 4 |
| 3 |
(3)证明:设Q1(x3,y3),Q2(x4,y4),过F点的直线l1为x=ky+1,代入抛物线方程得y2-4ky-2=0,
∴y3+y4=4k,y3y4=-2,
∴|P1P2|=x3+x4+2=k(y3+y4)+4=4k2+4,
同理|Q1Q2|=
| 4 |
| k2 |
∴
| 1 |
| |P1P2| |
| 1 |
| |Q1Q2| |
| 1 |
| 4 |
点评:本题考查抛物线的定义,考查直线与抛物线相交问题,考查向量知识,考查小时分析解决问题的能力,有难度.

练习册系列答案
相关题目
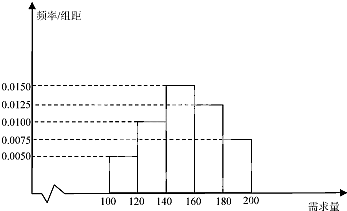 某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个丌学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个丌学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润. 如图,四棱锥P-ABCD的底面是边长为2的正方形,M是PC上一点,侧棱PA⊥底面ABCD,且PC与底面ABCD成45°角.
如图,四棱锥P-ABCD的底面是边长为2的正方形,M是PC上一点,侧棱PA⊥底面ABCD,且PC与底面ABCD成45°角. 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.