题目内容
5.某同学在独立完成课本上的例题:“求证:$\sqrt{3}$+$\sqrt{7}$<2$\sqrt{5}$”后,又进行了探究,发现下面的不等式均成立.$\sqrt{0}+\sqrt{10}<2\sqrt{5}$$\sqrt{1.3}+\sqrt{8.7}<2\sqrt{5}$
$\sqrt{2}+\sqrt{8}<2\sqrt{5}$
$\sqrt{4.6}+\sqrt{5.4}<2\sqrt{5}$
$\sqrt{5}+\sqrt{5}≤2\sqrt{5}$
经过认真地分析、尝试,该同学归纳出一个一般性的不等式:$\sqrt{x}$+$\sqrt{y}$≤2$\sqrt{\frac{x+y}{2}}$(x,y∈[0,+∞)).请用合适的方法证明该不等式成立.
分析 运用分析法证明,通过两边平方和完全平方公式,即可得证.
解答 证明:要证:$\sqrt{x}$+$\sqrt{y}$≤2$\sqrt{\frac{x+y}{2}}$(x,y≥0),
两边平方即证x+y+2$\sqrt{xy}$≤2(x+y),
即为x+y-2$\sqrt{xy}$≥0,
即有($\sqrt{x}$-$\sqrt{y}$)2≥0,
上式显然成立,且当且仅当x=y取得等号.
点评 本题考查归纳思想的运用以及不等式的证明,注意运用分析法证明,考查推理和归纳能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.已知13+23+33+…+n3=$\frac{{{n^2}{{(an+b)}^2}}}{4}$对一切n∈N+都成立,那么a,b的可能值为( )
| A. | a=b=1 | B. | a=1,b=2 | C. | a=2,b=1 | D. | 不存在这样的a,b |
13.为减少“舌尖上的浪费”,我校的学生会干部对一中,城关中学的食堂用餐的学生能否做到“光盘”进行调查.现从中随机抽取男、女生各25名进行问卷调查,得到了如下列联表:
(Ⅰ)补全相应的2×2列联表;
(Ⅱ)运用独立性检验的思想方法分析:能否在犯错误的概率不超过0.05的前提下认为在学校食堂用餐的学生能做到“光盘”与性别有关?并说明理由.
| 男性 | 女性 | 合计 | |
| 做不到“光盘” | 18 | ||
| 能做到“光盘” | 14 | ||
| 合 计 | 50 |
(Ⅱ)运用独立性检验的思想方法分析:能否在犯错误的概率不超过0.05的前提下认为在学校食堂用餐的学生能做到“光盘”与性别有关?并说明理由.
20.设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在[a,b]上两个不同的零点,则称f(x)与g(x)的“关联区间”,若f(x)=$\frac{1}{3}{x^3}-{x^2}$-x与g(x)=2x+b的“关联区间”是[-3,0],则b的取值范围是( )
| A. | [-9,0] | B. | $[0,\frac{5}{3}]$ | C. | $[-9,\frac{5}{3}]$ | D. | $[0,\frac{5}{3})$ |
10. 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )
①f(x)在(-3,1)上是增函数;
②x=-1是f(x)的极小值点;
③x=2是f(x)的极小值点;
④f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )①f(x)在(-3,1)上是增函数;
②x=-1是f(x)的极小值点;
③x=2是f(x)的极小值点;
④f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
| A. | ①②④ | B. | ②④ | C. | ③④ | D. | ①③④ |
14.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第2016个图案中的白色地面砖有( )
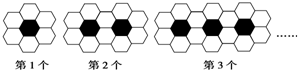

| A. | 8064块 | B. | 8066块 | C. | 8068块 | D. | 8070块 |