题目内容
10．
如图所示是y=f（x）的导数图象，则正确的判断是（ ）①f（x）在（-3，1）上是增函数；
②x=-1是f（x）的极小值点；
③x=2是f（x）的极小值点；
④f（x）在（2，4）上是减函数，在（-1，2）上是增函数．
| A． | ①②④ | B． | ②④ | C． | ③④ | D． | ①③④ |
分析 根据图象求出函数的单调区间，从而求出函数的极值点，进而得到答案．
解答 解：由图象得：f（x）在（-∞，-1）递减，在（-1，2）递增，在（2，4）递减，（4，+∞）递增，
∴x=4是f（x）的极小值点，x=2是f（x）的极大值点，
故②④正确，
故选：B．
点评 本题考察了函数的单调性，函数的极值问题，本题是一道基础题．
练习册系列答案
相关题目
20．已知定义在R上的可导函数f（x）图象既关于直线x=1对称，又关于直线x=5对称，且当x∈[1，5]时，有f′（x）＞3f（x），则下列各式成立的是（ ）
| A． | e3f（-14）＜f（-5），e3f（-10）＜f（-19） | B． | e3f（-14）＞f（-5），e3f（-10）＞f（-19） | ||
| C． | e3f（-14）＜f（-5），e3f（-10）＞f（-19） | D． | e3f（-14）＞f（-4），e3f（-10）＜f（-19） |
1．已知函数f（x）的导函数f′（x）=（1-x）e-x．若f（x）在（m，m+2）上单调递增，则实数m的取值范围是（ ）
| A． | [1，+∞） | B． | （-∞，1] | C． | [-1，+∞） | D． | （-∞，-1] |
18．若不等式|x+2|-|x-1|≥a3-4a2-3对任意实数x恒成立，则实数a的取值范围是（ ）
| A． | （-∞，4] | B． | （-∞，2] | C． | [4，+∞） | D． | [2，+∞） |
19．
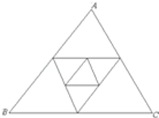如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（ ）
如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（ ）| A． | $\frac{1}{2002}$ | B． | $\frac{1}{2001}$ | C． | $\frac{1}{{2}^{2002}}$ | D． | 2${\;}^{\frac{1}{2001}}$ |