题目内容
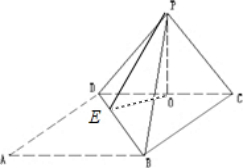
 如图,在矩形ABCD中,AB=4,BC=3,沿对角线BD将Rt△ABD折起,使点A到P点,且点P在平面BCD内的射影O恰好落在CD边上,求二面角P-BD-C的正弦值.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线BD将Rt△ABD折起,使点A到P点,且点P在平面BCD内的射影O恰好落在CD边上,求二面角P-BD-C的正弦值.考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:过点O作OE⊥BD,连结PE,可得∠PEO为二面角P-BD-C的平面角,解△CPD和△DPB,可得答案
解答:
 解:∵PO⊥面BCD,
解:∵PO⊥面BCD,
∴过点O作OE⊥BD,连结PE,PE⊥BD,
∴∠PEO为二面角P-BD-C的平面角,
∵四边形ABCD为矩形,
∴BC⊥CD,DA⊥AB,
∵A点移动到了P点,
∴PD⊥PB,
又∵P点在平面BCD上的射影在CD上,
∴过P点作PO⊥CD,
∴PO⊥面BCD,
∴BC⊥面PCD,
∴PD⊥面PBC,
∴PD⊥PC,
∴△CPD为Rt△,
∵AB=4,BC=3,BD=
=3
.PE=
=
=
.
∴PC=
=
,
在Rt△DPC中,DC•PO=PD•PC,
解得:PO=
=
.
∴sin∠PEO=
=
=
,
二面角P-BD-C的正弦值:
.
 解:∵PO⊥面BCD,
解:∵PO⊥面BCD,∴过点O作OE⊥BD,连结PE,PE⊥BD,
∴∠PEO为二面角P-BD-C的平面角,
∵四边形ABCD为矩形,
∴BC⊥CD,DA⊥AB,
∵A点移动到了P点,
∴PD⊥PB,
又∵P点在平面BCD上的射影在CD上,
∴过P点作PO⊥CD,
∴PO⊥面BCD,
∴BC⊥面PCD,
∴PD⊥面PBC,
∴PD⊥PC,
∴△CPD为Rt△,
∵AB=4,BC=3,BD=
| AB2+BC2 |
| 5 |
| AQ•AB |
| BD |
| 3×6 | ||
3
|
6
| ||
| 5 |
∴PC=
| PB2-BC2 |
| 37 |
在Rt△DPC中,DC•PO=PD•PC,
解得:PO=
3×
| ||
| 6 |
| ||
| 2 |
∴sin∠PEO=
| PO |
| PE |
| ||||
|
| ||
| 12 |
二面角P-BD-C的正弦值:
| ||
| 12 |
点评:本题考查的知识点是二面角的平面角及求法,是空间立体几何的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知命题p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≤0,则( )
| A、¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an≤0 |
| B、¬p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an>0 |
| C、¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an>0 |
| D、¬p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≥0 |
若点(1,2)到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、-2或2 | ||||
B、
| ||||
| C、2或0 | ||||
| D、-2或0 |
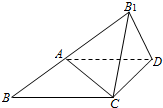 已知四边形ABCD是矩形,BC=
已知四边形ABCD是矩形,BC=