题目内容
1.已知三点P1(1,1,0),P2(0,1,1)和P3(1,0,1),O是坐标原点,则|$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$|=( )| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | 12 |
分析 求出向量的和,然后求解向量的模即可.
解答 解:三点P1(1,1,0),P2(0,1,1)和P3(1,0,1),O是坐标原点,
则$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=(2,2,2).
则|$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$|=$\sqrt{{2}^{2}+{2}^{2}+{2}^{2}}$=2$\sqrt{3}$.
故选:C.
点评 本题考查空间向量的模,空间两点间距离公式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.化简$\sqrt{1-{{sin}^2}{{140}°}}$=( )
| A. | ±cos40° | B. | cos40° | C. | -cos40° | D. | ±|cos40°| |
11.已知P是直线kx+4y-10=0(k>0)上的动点,是圆C:x2+y2-2x+4y+4=0的两条切线,A,B是切点,C是圆心,若四边形PACB面积的最小值为$2\sqrt{2}$,则k的值为( )
| A. | 3 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{15}{2}$ |
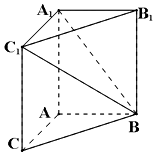 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.