题目内容

15．若向量$\overrightarrow a=（1，1）$，$\overrightarrow b=（2，5）$，$\overrightarrow c=（x，4）$，满足条件$（8\overrightarrow a-\overrightarrow b）•\overrightarrow c=30$，则x等于（　　）
A．6B．5C．4D．3

分析 由向量的加减运算可得8$\overrightarrow{a}$-$\overrightarrow{b}$，运用向量数量积的坐标表示，解方程即可得到x的值．

解答 解：∵向量$\overrightarrow a=（1，1）$，$\overrightarrow b=（2，5）$，$\overrightarrow c=（x，4）$，
∴8$\overrightarrow{a}$-$\overrightarrow{b}$=（8，8）-（2，5）=（6，3），
又∵$（8\overrightarrow a-\overrightarrow b）•\overrightarrow c=30$，
∴（6，3）•（x，4）=6x+12=30，
∴x=3，
故选D．

点评 本题考查向量的加减运算和向量数量积的坐标表示，考查方程思想，以及化简整理的运算能力，属于基础题．

练习册系列答案
相关题目
5．已知logax=2，logbx=3，则logabx=$\frac{6}{5}$．
6．某地震观测站对地下水位的变化和发生地震的情况共进行了n=1 700次观测，列联表如下：
Y
X		有震无震合计
水位有变化1009001 000
水位无变化806207 00
合计18015201700
问观测结果是否说明地下水位的变化与地震的发生相关？
P（X2≥x0）0.150.10.05
x02.0722.7063.841
3．已知抛物线y2=8x的焦点恰好是椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞0）的右焦点，则椭圆方程为$\frac{{x}^{2}}{5}+{y}^{2}=1$．
10．已知定义在R上的函数y=f（x）满足函数y=f（x-1）的图象关于直线x=1对称，且当x∈（-∞，0），f（x）+xf'（x）＜0成立（f'（x）是函数f（x）的导数），若$a=\frac{1}{2}f（{{{log}_2}\sqrt{2}}），b=（{ln2}）f（{ln2}），c=2f（{{{log}_{\frac{1}{2}}}\frac{1}{4}}）$，则a，b，c的大小关系是（　　）
A．a＞b＞cB．b＞a＞cC．c＞a＞bD．a＞c＞b
20．三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD=PC=4，$AB=4\sqrt{2}$，BC=3．点E是CD边的中点，点F、G分别在线段AB、BC上，且AF=2FB，CG=2GB．
（1）证明：BC∥平面PDA；
（2）求二面角P-AD-C的大小；
（3）求直线PA与直线FG所成角的余弦值．
7．已知x∈（0，2），关于x的不等式$\frac{x}{{e}^{x}}$＜$\frac{1}{k+2x-{x}^{2}}$恒成立，则实数k的取值范围为[0，e-1）．
4．具有性质：f（$\frac{1}{x}$）=-f（x）的函数，我们称为满足“倒负”变换的函数．给出下列函数：
①y=ln$\frac{1-x}{1+x}$；②y=$\frac{{1-{x^2}}}{{1+{x^2}}}$；③y=$\left\{{\begin{array}{l}{x，0＜x＜1}\\{0，x=1}\\{-\frac{1}{x}，x＞1}\end{array}}$
其中满足“倒负”变换的函数是（　　）
A．①②B．①③C．②③D．①
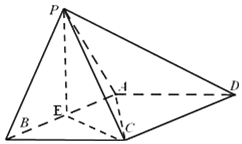5．已知四棱锥P-ABCD，底面ABCD为菱形，∠ABC=60°，△PAB是等边三角形，AB=2，PC=$\sqrt{6}$，AB的中点为E
（1）证明：PE⊥平面ABCD；
（2）求三棱锥D-PBC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网