题目内容
13.已知函数f(x)=ax3+bx+1的图象经过点(1,-3)且在x=1处f(x)取得极值.求:(1)函数f(x)的解析式;
(2)f(x)的单调递增区间.
分析 (1)代入点的坐标,求出导函数,解方程组可得a,b值;
(2)求出导函数,利用导函数得出函数的单调递增区间.
解答 解:(1)由f(x)=ax3+bx+1的图象过点(1,-3)得f(1)=a+b+1=3,
∵f'(x)=3ax2+b,
又f'(1)=3a+b=0,
∴a=2,b=-6,
∴f(x)=2x3-6x+1.
(2)∵f'(x)=6x2-6,
∴由f'(x)>0得x>1或x<-1,
∴f(x)的单调递增区间为(-∞,-1)和(1,+∞).
点评 本题考查了函数的基本性质和利用导函数判断函数的单调区间.属于基础题型,应熟练掌握.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
8.若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,-2),则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{17}$ | B. | 1 | C. | $\sqrt{7}$ | D. | $\sqrt{15}$ |
18.某程序框图如图所示,当输入x的值是1时,输出y的值是( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
2.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
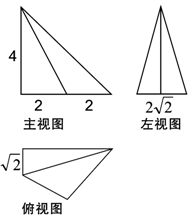

| A. | 136π | B. | 144π | C. | 36π | D. | 34π |
3.执行如图所示的程序框图,输出的结果为( )
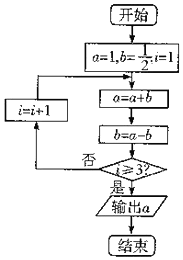

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈(0,1),给出以下命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈(0,1),给出以下命题: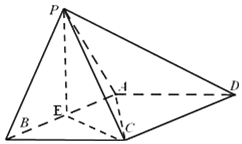 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E