题目内容
已知函数f(x)=
+2ln(x-1),求函数f(x)的极值.
| 1 |
| (1-x)2 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:利用导数判断函数的单调性进而求出函数的极值.
解答:
解:∵f(x)=
+2ln(x-1),
∴函数f(x)的定义域是(1,+∞),
又f′(x)=
+
=
,
∴x∈(1,2)时,f′(x)<0,x∈(2,+∞)时,f′(x)>0,
∴当x=2时,f(x)有极小值为f(2)=1.
| 1 |
| (1-x)2 |
∴函数f(x)的定义域是(1,+∞),
又f′(x)=
| 2 |
| (1-x)3 |
| 2 |
| x-1 |
| 2x(x-2) |
| (x-1)3 |
∴x∈(1,2)时,f′(x)<0,x∈(2,+∞)时,f′(x)>0,
∴当x=2时,f(x)有极小值为f(2)=1.
点评:本题考查利用导数研究函数的极值知识,属基础题.

练习册系列答案
相关题目
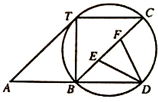 如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.
如图,⊙O过平行四边形ABCT的三个顶点B,C,T,且与AT相切,交AB的延长线于点D.