题目内容
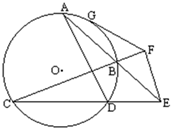延长图O的两弦AB，CD交于圆外一点E，过E点作DA的平行线交CB的廷长线于点F，自F点作图0的切线FG．求证FG=FE．考点：与圆有关的比例线段
专题：立体几何
分析：由已知得∠FEB=∠BAD，从而∠FEB=∠BCD，又∠EFB=∠EFC，从而△EFB∽△CFE，由此求出FE2=FB•FC．从而得到FG=FE．
解答：
证明：∵EF∥DA，
∴∠FEB=∠BAD，而∠BAD=∠BCD，
∴∠FEB=∠BCD，又∠EFB=∠EFC
∴△EFB∽△CFE
因此，FE：FC=FB：FE，
即FE2=FB•FC．
∵FG是圆O的切线，FBC的圆O的割线，
∴FG2=FB•FC
∴FG2=FE2，
故FG=FE．
∴∠FEB=∠BAD，而∠BAD=∠BCD，
∴∠FEB=∠BCD，又∠EFB=∠EFC
∴△EFB∽△CFE
因此，FE：FC=FB：FE，
即FE2=FB•FC．
∵FG是圆O的切线，FBC的圆O的割线，
∴FG2=FB•FC
∴FG2=FE2，
故FG=FE．
点评：本题考查线段长相等的证明，是中档题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目