题目内容

已知f（cosx）=2-sin2x，则f（sinx）=
 
．
考点：二倍角的正弦,函数解析式的求解及常用方法
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系，二倍角的正弦公式求得f（sinx）．
解答： 解：∵f（cosx）=2-sin2x=2-2sinxcosx=2-2
1-cos2x
cosx，
∴f（t）=2-2t
1-t2
，
∴f（sinx）=2-2
1-sin2x
sinx=2-2sinxcosx=2-sin2x，
故答案为：2-sin2x．
点评：本题主要考查同角三角函数的基本关系，二倍角的正弦公式，属于基础题．
练习册系列答案
相关题目
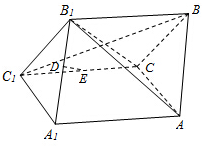如图，四边形A A1 C1C为矩形，四边形CC1B1 B为菱形，且平面CC1B1 B⊥A A1 C1C，D，E分别是A1 B1和C1C的中点．求证：（1）BC1⊥平面AB1C；
（2）DE∥平面AB1C．
已知数列{an}的前n项和为Sn，且a1=2，a2=8，a3=24，{an+1-2an}为等比数列．
（1）求证：{
an
2n
}是等差数列
（2）求
1
Sn
的取值范围．
设α∈（0，π），且α≠
π
2
，当∠xOy=α时，定义坐标系xOy为α-仿射坐标（如图），在α-仿射坐标系中，任意一点P的坐标这样定义“
e1
，
e2
分别是与x轴，y轴方向同向的单位向量，若向量
OP
=x
e1
+y
e2
，则记
OP
=（x，y），下列结论正确的是
 
（写上所有正确结论的序号）
①设向量
α
=（m，n），
b
=（s，t），若
α
=
b
，则有m=m，s=t；
②设向量
α
=（m，n），则|
α
|=
m2+n2
；
③设向量
α
=（m，n）
b
=（s，t），若
α
∥
b
，则有mt-ns=0；
④设向量
α
=（m，n）
b
=（s，t），若
α
⊥
b
，则有mt+ns=0；
⑤设向量
α
=（1，2）
b
=（2，1），若
α
与
b
的夹角为
π
3
，则有α=
2π
3
．
质检大队对某超市一项产品进行检验，该产品成箱包装，每箱5件．抽检人员前先取出3箱，再从每箱中任意抽取2件产品进行检验，设取出的三箱中分别有1件、l件、2件二等品，其余为一等品．
（1）求抽检的6件产品中有2件或2件以上二等品的概率；
（2）用ξ表示抽检的6件产品中二等品的件数，求随机变量ξ的分布列及数学期望．
若sin（α+β）=2sinα，且α，β均为锐角，求证：α＜β
设sinθ，cosθ使方程2x2-（
3
+1）x+2m=0的两根，求m与
sinθ
1-cotθ
+
cosθ
1-tanθ
的值．
如图是一个算法的程序框图，最后输出的W是（　　）
A、22B、23C、24D、25
已知各项均不为零的数列{an}满足Sn=
a
a-1
(an-1)（a为非零常数且a≠1）
（1）求{an}的通项公式；
（2）若bn=
2Sn
an
+1，且b1，b2，b3成等比数列，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网