题目内容
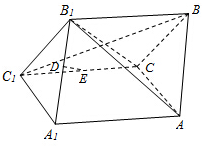 如图,四边形A A1 C1C为矩形,四边形CC1B1 B为菱形,且平面CC1B1 B⊥A A1 C1C,D,E分别是A1 B1和C1C的中点.求证:(1)BC1⊥平面AB1C;
如图,四边形A A1 C1C为矩形,四边形CC1B1 B为菱形,且平面CC1B1 B⊥A A1 C1C,D,E分别是A1 B1和C1C的中点.求证:(1)BC1⊥平面AB1C;(2)DE∥平面AB1C.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用面面垂直的性质定理,得到AC⊥平面CC1B1 B,再由线面垂直的性质得到AC⊥BC1,进一步利用菱形的性质得到B1C⊥BC1,利用线面垂直的判定定理可证;
(2)取AA1的中点,连接DF,EF,分别判断EF,DF与平面平面AB1C平行,得到面面平行,利用面面平行的性质可证.
(2)取AA1的中点,连接DF,EF,分别判断EF,DF与平面平面AB1C平行,得到面面平行,利用面面平行的性质可证.
解答:
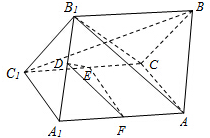 解:(1)∵四边形A A1 C1C为矩形,∴AC⊥CC1,
解:(1)∵四边形A A1 C1C为矩形,∴AC⊥CC1,
又平面CC1B1 B⊥A A1 C1C,CC1B1 B∩A A1 C1C=CC1,
∴AC⊥平面CC1B1 B,
∵BC1?平面CC1B1 B,
∴AC⊥BC1,
∵四边形CC1B1 B为菱形,∴B1C⊥BC1,
又B1C∩AC=C,AC?平面A1C,B1C?平面AB1C,
∴BC1⊥平面AB1C;
(2)取AA1的中点,连接DF,EF,
∵四边形A A1 C1C为矩形,E,F分别是C1C,AA1的中点,
∴EF∥AC,又EF?平面平面AB1C,AC?平面AB1C,
∴EF∥平面AB1C,
又D,F分别是A1 B1和AA1的中点,
∴DF∥A B1,
又DF?平面AB1C,AB1?平面AB1C,
∴DF∥平面AB1C,
∵EF∩DF=F,EF?平面DEF,DF?平面DEF,
∴平面DEF∥平面AB1C,
∵DE?平面DEF,
∴DE∥平面AB1C.
 解:(1)∵四边形A A1 C1C为矩形,∴AC⊥CC1,
解:(1)∵四边形A A1 C1C为矩形,∴AC⊥CC1,又平面CC1B1 B⊥A A1 C1C,CC1B1 B∩A A1 C1C=CC1,
∴AC⊥平面CC1B1 B,
∵BC1?平面CC1B1 B,
∴AC⊥BC1,
∵四边形CC1B1 B为菱形,∴B1C⊥BC1,
又B1C∩AC=C,AC?平面A1C,B1C?平面AB1C,
∴BC1⊥平面AB1C;
(2)取AA1的中点,连接DF,EF,
∵四边形A A1 C1C为矩形,E,F分别是C1C,AA1的中点,
∴EF∥AC,又EF?平面平面AB1C,AC?平面AB1C,
∴EF∥平面AB1C,
又D,F分别是A1 B1和AA1的中点,
∴DF∥A B1,
又DF?平面AB1C,AB1?平面AB1C,
∴DF∥平面AB1C,
∵EF∩DF=F,EF?平面DEF,DF?平面DEF,
∴平面DEF∥平面AB1C,
∵DE?平面DEF,
∴DE∥平面AB1C.
点评:本题考查直线与平面的垂直的判定、直线与平面平行的判定,体现了转化的思想,考查逻辑思维能力 空间想象能力,是中档题.

练习册系列答案
相关题目
已知某离散型随机变量?分布列如下,则常数k的值为( )
| ? | 1 | 2 | 3 | … | n |
| P | k | 3k | 5k | … | (2n-1)k |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
+
=1(m>0,n>0),则当m+n取得最小值时,椭圆
+
=1的离心率为( )
| 1 |
| m |
| 2 |
| n |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|