题目内容
若A={x|-2≤x≤3},B={x|2m-1≤x≤m+1},
(1)当B⊆A时,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
(1)当B⊆A时,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:(1)根据已知条件,讨论B=∅,和B≠∅两种情况,B=∅时,得到m>2;B≠∅时,得到-
≤m≤2,这样便求出了m的范围;
(2)根据已知条件知:A∩B=∅,所以讨论B=∅,和B≠∅.B=∅时,由(1)已经求出,B≠∅时,写出限制a的不等式,解不等式即可,这两种情况的m求并集即可.
| 1 |
| 2 |
(2)根据已知条件知:A∩B=∅,所以讨论B=∅,和B≠∅.B=∅时,由(1)已经求出,B≠∅时,写出限制a的不等式,解不等式即可,这两种情况的m求并集即可.
解答:
解:(1)B⊆A,若B=∅,则2m-1>m+1,∴m>2;
若B≠∅,则
,解得-
≤m≤2;
∴实数m的取值范围是[-
,+∞);
(2)根据已知条件知:A∩B=∅;
∴若B=∅,由(1)知,m>2;
若B≠∅,则
,解得m<-3;
∴实数m的取值范围为(-∞,-3)∪(2,+∞).
若B≠∅,则
|
| 1 |
| 2 |
∴实数m的取值范围是[-
| 1 |
| 2 |
(2)根据已知条件知:A∩B=∅;
∴若B=∅,由(1)知,m>2;
若B≠∅,则
|
∴实数m的取值范围为(-∞,-3)∪(2,+∞).
点评:考查子集、空集的概念,交集的概念,注意不要漏了B=∅的情况.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
下列说法中不正确的是( )
A、对于线性回归方程
| ||||||||||
| B、茎叶图的优点在于它可以保存原始数据,并且可以随时记录 | ||||||||||
| C、将一组数据中的每一个数据都加上或减去同一常数后,方差恒不变 | ||||||||||
| D、掷一枚均匀硬币连续出现5次正面,第6次掷这枚硬币一定出现反面 |
已知等比数列{an}的前n项和为Sn,若S4=1,S12=13,则a13+a14+a15+a16=( )
| A、27 | B、64 |
| C、-64 | D、27或-64 |
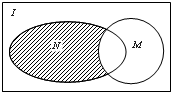 设全集I是实数集R.M={x|x>2或x<-2}与N={x|1<x<3}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R.M={x|x>2或x<-2}与N={x|1<x<3}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A、{x|x<2} |
| B、{x|-2≤x<1} |
| C、{x|1<x≤2} |
| D、{x|-2≤x≤2} |
椭圆9x2+y2=9的长轴长为( )
| A、2 | B、3 | C、6 | D、9 |
已知集合M={x|-x2+2x>0},N={x|
<1},则M∩N等于( )
| x |
| x-1 |
| A、(0,2) |
| B、(0,1) |
| C、(1,2) |
| D、(-1,1) |