题目内容
2.在直角坐标系xOy中,直线l的方程是y=8,圆C的参数方程是$\left\{\begin{array}{l}{x=2+2cosφ}\\{y=2sinφ}\end{array}\right.$(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.(1)求直线l和圆C的极坐标方程;
(2)射线OM:θ=α(其中0<α<$\frac{π}{2}$)与圆C交于O,P两点,与直线l交于点M,直线ON:θ=α+$\frac{π}{2}$与圆C交于O,Q两点,与直线l交于点N,求$\frac{|OP|}{|OM|}•\frac{|OQ|}{|ON|}$的最大值.
分析 (1)直线l的方程是y=8,利用y=ρsinθ即可化为极坐标方程.
圆C的参数方程是$\left\{\begin{array}{l}{x=2+2cosφ}\\{y=2sinφ}\end{array}\right.$(φ为参数),化为普通方程:x2+y2-4x=0,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\\{{ρ}^{2}={x}^{2}+{y}^{2}}\end{array}\right.$即可化为极坐标方程.
2)$\frac{|OP|}{|OM|}•\frac{|OQ|}{|ON|}$=$\frac{4cosα}{\frac{8}{sinα}}$•$\frac{-4cos(α+\frac{π}{2})}{\frac{8}{sin(α+\frac{π}{2})}}$=$\frac{1}{16}si{n}^{2}(2α)$(2α∈(0,π)).即可得出.
解答 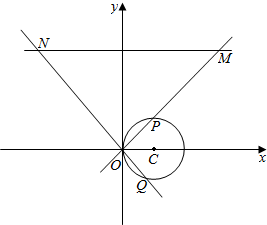 解:(1)直线l的方程是y=8,化为极坐标方程为:ρsinθ=8.
解:(1)直线l的方程是y=8,化为极坐标方程为:ρsinθ=8.
圆C的参数方程是$\left\{\begin{array}{l}{x=2+2cosφ}\\{y=2sinφ}\end{array}\right.$(φ为参数),化为普通方程:(x-2)2+y2=4,
展开为:x2+y2-4x=0,化为极坐标方程:ρ2-4ρcosθ=0,即ρ=4cosθ.
(2)$\frac{|OP|}{|OM|}•\frac{|OQ|}{|ON|}$=$\frac{4cosα}{\frac{8}{sinα}}$•$\frac{-4cos(α+\frac{π}{2})}{\frac{8}{sin(α+\frac{π}{2})}}$=$\frac{1}{16}si{n}^{2}(2α)$≤$\frac{1}{16}$(2α∈(0,π)).
∴$\frac{|OP|}{|OM|}•\frac{|OQ|}{|ON|}$的最大值为$\frac{1}{16}$.
点评 本题考查了极坐标系下的直线与曲线相交弦长问题、参数方程化为普通方程、极坐标方程化为直角坐标方程,考查了推理能力与计算能力,属于中档题.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | (-∞,-3]∪(1,+∞) | B. | (-∞,-3]∪(-1,+∞) | C. | (-∞,1)∪[3,+∞) | D. | (-∞,-1)∪[3,+∞) |
| A. | -6 | B. | -4 | C. | 4 | D. | 6 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
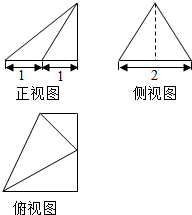 某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.
某几何体的三视图(单位:cm)如图所示,其中侧视图是一个边长为2的正三角形,则这个几何体的体积为$\sqrt{3}$.