题目内容
14．
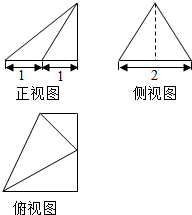某几何体的三视图（单位：cm）如图所示，其中侧视图是一个边长为2的正三角形，则这个几何体的体积为$\sqrt{3}$．
分析 几何体为四棱锥，棱锥底面为直角梯形，棱锥的高为侧视图三角形的高．
解答 解：由三视图可知几何体为四棱锥，棱锥的底面为俯视图中的直角梯形，棱锥的高为侧视图三角形的高．
∵侧视图为等边三角形，边长为2，所以侧视图三角形的高为$\sqrt{3}$，即棱锥的高为$\sqrt{3}$．
由三视图的对应关系可知俯视图中直角梯形的上下底分别是1，2，直腰为2．
∴四棱锥的体积V=$\frac{1}{3}×\frac{1}{2}×（1+2）×2×\sqrt{3}$=$\sqrt{3}$．
故答案为$\sqrt{3}$．
点评 本题考查了棱锥的三视图和结构特征，体积计算，属于基础题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
5．已知函数f（x）=2sinxcosx-$\sqrt{3}$cos2x．
（1）求f（x）的最小正周期和单调递增区间；
（2）当x∈$[0，\frac{π}{2}]$时，求函数f（x）的最大值和最小值．
（1）求f（x）的最小正周期和单调递增区间；
（2）当x∈$[0，\frac{π}{2}]$时，求函数f（x）的最大值和最小值．
9．函数f（x）=3sinx-log2x的零点个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
19．某大学餐饮中心为了解新生的饮食习惯，在全校一年级学生中进行了抽样调查，调查结果如表所示：
（1）根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
（2）已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取2人，求恰有1人喜欢甜品的概率．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（a+c）（b+d）（c+d）}$，
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 40 | 20 | 60 |
| 北方学生 | 20 | 20 | 40 |
| 合计 | 60 | 40 | 100 |
（2）已知在被调查的北方学生中有5名数学系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取2人，求恰有1人喜欢甜品的概率．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（a+c）（b+d）（c+d）}$，
| P（K2≥k） | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |