题目内容
11.用大小完全相同的黑、白两种颜色的正六边形积木拼成如图所示的图案,按此规律再拼5个图案,并将这8个图案中的所有正六边形积木充分混合后装进一个盒子中,现从盒子中随机取出一个积木,则取出黑色积木的概率是$\frac{9}{49}$.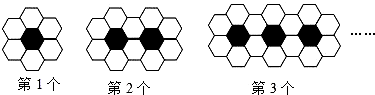
分析 由图形可知各图形中的黑色积木和白色积木分别成等差数列,求出积木总个数,使用古典概型的概率计算公式计算概率.
解答 解:由图可知第1个图形由1个黑色积木,6个白色积木,第二个图形有2个黑色积木,10个白色积木,第三个图形有3个黑色积木,14个白色积木,
依此类推,故图形中的黑色积木数组成一个等差数列,公差为1,白色积木数组成一个等差数列,公差为4.
从而前8个图形共有黑色积木个数为8×1+$\frac{8×7}{2}×1$=36,共有白色积木个数为8×6+$\frac{8×7}{2}×4$=160.
∴取出黑色积木的概率P=$\frac{36}{36+160}$=$\frac{9}{49}$.
故答案为$\frac{9}{49}$.
点评 本题考查了归纳推理,古典概型的概率计算,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
1.下列各点中,可作为函数y=tanx的对称中心的是( )
| A. | ($\frac{π}{4}$,0) | B. | ($\frac{π}{4}$,1) | C. | (-$\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
19.某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如表所示:
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取2人,求恰有1人喜欢甜品的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(b+d)(c+d)}$,
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 40 | 20 | 60 |
| 北方学生 | 20 | 20 | 40 |
| 合计 | 60 | 40 | 100 |
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取2人,求恰有1人喜欢甜品的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(b+d)(c+d)}$,
| P(K2≥k) | 0.10 | 0.05 | 0.01 |
| k | 2.706 | 3.841 | 6.635 |
