题目内容
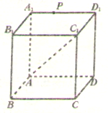 如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是
如图,P是正方体ABCD-A1B1C1D1上一动点,设点P和直线AC1确定的平面为α,过点P与直线AC1垂直的平面为β,则下列命题正确的序号是①α⊥β;
②平面α将正方体分割为体积相等的两部分;
③β截正方体所得截面多边形可能是四边形;
④β截正方体所得截面多边形的面积是定值;
⑤当且仅当P是A1D1的中点时,α截正方体所得截面多边形周长最小.
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:由面面垂直的判定定理可判断①;运用正方体的对称性即可判断②;可根据截面A1BD和截面B1CD1都和直线AC1垂直,可知β截正方体所得截面介于截面A1BD和截面B1CD1之间,从而判断③;可考虑P为中点时的截面面积,可判断④;延长DD1至点E,使得DD1=D1E,讨论P为中点时的截面周长,可判断⑤.
解答:
 解:①因为平面α过AC1,且AC1⊥β,
解:①因为平面α过AC1,且AC1⊥β,
所以α⊥β,故①正确;
②由于平面α经过直线AC1,
由对称性易知②正确;
③由于AC1⊥截面A1BD和AC1⊥截面B1CD1,
β截正方体所得截面介于截面A1BD和
截面B1CD1之间,可以是三角形或六边形,
故③错;
④当P为A1D1的中点时的截面面积与三角形A1BD的面积显然不等,故④错;
⑤延长DD1至点E,使得DD1=D1E,
则有AP+PC1=AP+EP≥AE,
当且仅当P是A1D1的中点时,等号成立,
此时结合对称性知截面多边形的周长最小,
故⑤正确.
故答案为:①②⑤.
 解:①因为平面α过AC1,且AC1⊥β,
解:①因为平面α过AC1,且AC1⊥β,所以α⊥β,故①正确;
②由于平面α经过直线AC1,
由对称性易知②正确;
③由于AC1⊥截面A1BD和AC1⊥截面B1CD1,
β截正方体所得截面介于截面A1BD和
截面B1CD1之间,可以是三角形或六边形,
故③错;
④当P为A1D1的中点时的截面面积与三角形A1BD的面积显然不等,故④错;
⑤延长DD1至点E,使得DD1=D1E,
则有AP+PC1=AP+EP≥AE,
当且仅当P是A1D1的中点时,等号成立,
此时结合对称性知截面多边形的周长最小,
故⑤正确.
故答案为:①②⑤.
点评:本题主要考查空间直线与平面的位置关系,考查线面垂直、面面垂直的判定,同时考查空间想象能力和判断能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知集合A={-2,0,2},B={x|x2-x-2=0},则A∩B=( )
| A、∅ | B、{2} |
| C、{0} | D、{-2} |
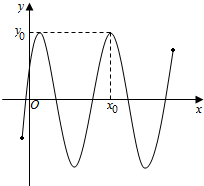 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+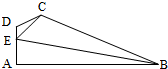 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=