题目内容
已知复数z满足z+i-3=3-i，则z的实部、虚部分别是（ ） （i为虚数单位）
| A、6，-2 | B、6，-2i |
| C、0，-2 | D、0，-2i |
考点：复数的基本概念
专题：计算题,数系的扩充和复数
分析：设z=a+bi（a，b∈R），由z+i-3=3-i可化为a-3+（b+1）i=3-i，则
，解出即可．
|
解答：
解：设z=a+bi（a，b∈R），
则z+i-3=3-i可化为a-3+（b+1）i=3-i，
∴
，解得
，
故选A．
则z+i-3=3-i可化为a-3+（b+1）i=3-i，
∴
|
|
故选A．
点评：本题考查复数的基本概念，属基础题，准确理解复数相等的概念是解题关键．
练习册系列答案
相关题目
一只艘船以均匀的速度由A点向正北方向航行，如图，开始航行时，从A点观测灯塔C的方位角（从正北方向顺时针转到目标方向的水平角）为45°，行驶60海里后，船在B点观测灯塔C的方位角为75°，则A到C的距离是（ ）海里．A、30（
| ||||
B、30（
| ||||
C、30（
| ||||
D、30（
|
等差数列{an}，{bn}的前n项和分别为Sn，Tn，若
=
，则an=bn时n=（ ）
| Sn |
| Tn |
| 2n+4 |
| 3n+1 |
| A、无解 | B、6 | C、2 | D、无数多个 |
下列命题正确的是（ ）
| A、如果a，b是两条直线，且a∥b，那么a平行于经过b的任何平面 |
| B、如果直线a和平面α满足a∥α，那么a与α内的任何直线平行 |
| C、如果直线a，b和平面α满足a∥α，b∥α，那么a∥b |
| D、如果直线a，b和平面α满足a∥b，a∥α，b?α，那么b∥α |
抛物线y2=8x与双曲线
-
=1的一个焦点重合，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
已知双曲线
-
=1(b＞a＞0)的两条渐近线为l1，l2，过右焦点F作垂直l1的直线交l1，l2于A，B两点．若|OA|，|AB|，|OB|成等差数列，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
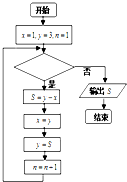已知数列{an}满足a1=1，a2=3，an+2=an+1-an，n∈N*，利用如图所示的程序框图计算该数列的第n项（n≥3），若输出S的结果为1，则判断框内的条件可能是（ ）| A、n≤5？ | B、n≤6？ |
| C、n≤7？ | D、n≤8？ |