题目内容
2.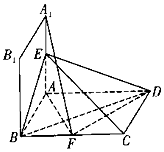 如图,边长为2的正方形A1ABB1所在平面与矩形ABCD所在平面相互垂直,且$AB=\frac{1}{2}BC$,E,F分别是AA1和BC的中点.
如图,边长为2的正方形A1ABB1所在平面与矩形ABCD所在平面相互垂直,且$AB=\frac{1}{2}BC$,E,F分别是AA1和BC的中点.(1)证明:DF⊥平面A1AF;
(2)求三棱锥C-BDE的体积.
分析 (1)推导出A1A⊥DF,AF⊥DF,由此能证明DF⊥平面A1AF.
(2)三棱锥C-BDE的体积VC-BDE=VE-BCD=VE-ABD.由此能求出结果.
解答 (本小题满分12分)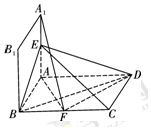
证明:(1)如图,∵平面A1ABB1⊥平面ABCD,A1A⊥AB,
∴A1A⊥平面ABCD,
∴A1A⊥DF,…(3分)
∵$AB=\frac{1}{2}BC$,∴AD=BC=4,BF=FC=2,
∵AB=BF=DC=2,∴$AF=DF=2\sqrt{2}$,
∵AD2=AF2+DF2,∴AF⊥DF.
∵A1A∩AF=A,∴DF⊥平面A1AF.…(6分)
解:(2)∵E为A1A的中点,∴AE=1,
∴三棱锥C-BDE的体积${V_{C-BDE}}={V_{E-BCD}}={V_{E-ABD}}=\frac{1}{3}×\frac{1}{2}×AB×AD×AE=\frac{1}{3}×\frac{1}{2}×2×4×1=\frac{4}{3}$.…(12分)
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
10.已知命题p:x2+x-2>0,命题q:{x|f(x)=lg(2x-3)},则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知底面边长为$2\sqrt{3}$的正三棱锥O-ABC的体积为$\sqrt{3}$,且A,B,C在球O上,则球的体积是( )
| A. | $\frac{{20\sqrt{5}π}}{3}$ | B. | 8π | C. | 20π | D. | $4\sqrt{3}π$ |
7.如果θ是第三象限的角,那么( )
| A. | sinθ>0 | B. | cosθ>0 | C. | tanθ>0 | D. | 以上都不对 |
14.设向量$\overrightarrow{a}$,$\overrightarrow{b}$的模分别为2和3,且夹角为60°,则|$\overrightarrow{a}$+$\overrightarrow{b}$|等于( )
| A. | $\sqrt{13}$ | B. | 13 | C. | $\sqrt{19}$ | D. | 19 |
11.函数y=a|sinx|+2(a>0)的单调递增区间是( )
| A. | (-$\frac{π}{2}$,$\frac{π}{2}$) | B. | (-π,-$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
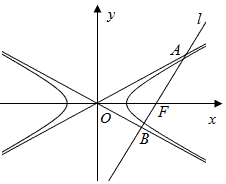 如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.
如图所示,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,过F的直线l交双曲线的渐近线于A,B两点,且直线l的倾斜角是渐近线OA倾斜角的2倍,若$\overrightarrow{AF}=2\overrightarrow{FB}$,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.