题目内容
15.设点M是x轴上的一个定点,其横坐标为a(a∈R),已知当a=1时,动圆N过点M且与直线x=-1相切,记动圆N的圆心N的轨迹为C.(Ⅰ)求曲线C的方程;
(Ⅱ)当a>2时,若直线l与曲线C相切于点P(x0,y0)(y0>0),且l与以定点M为圆心的动圆M也相切,当动圆M的面积最小时,证明:M、P两点的横坐标之差为定值.
分析 (Ⅰ)通过圆N与直线x=-1相切,推出点N到直线x=-1的距离等于圆N的半径,说明点N的轨迹为以点M(1,0)为焦点,直线x=-1为准线的抛物线,求出轨迹方程.
(Ⅱ)设直线l的方程为y-y0=k(x-x0),联立$\left\{\begin{array}{l}y-{y_0}=k(x-{x_0})\\{y^2}=4x\end{array}\right.$得$\frac{k}{4}{y^2}-y-k{x_0}+{y_0}=0$,利用相切关系,推出k,求解直线l的方程为$4x-2{y_0}y+{y_0}^2=0$.通过动圆M的半径即为点M(a,0)到直线l的距离$d=\frac{{|4a+{y_0}^2|}}{{\sqrt{16+4{y_0}^2}}}$.
利用动圆M的面积最小时,即d最小,然后求解即可.
解答 解:(Ⅰ)因为圆N与直线x=-1相切,所以点N到直线x=-1的距离等于圆N的半径,
所以,点N到点M(1,0)的距离与到直线x=-1的距离相等.
所以,点N的轨迹为以点M(1,0)为焦点,直线x=-1为准线的抛物线,
所以圆心N的轨迹方程,即曲线C的方程为y2=4x.
(Ⅱ)由题意,直线l的斜率存在,设直线l的方程为y-y0=k(x-x0),
由$\left\{\begin{array}{l}y-{y_0}=k(x-{x_0})\\{y^2}=4x\end{array}\right.$得$\frac{k}{4}{y^2}-y-k{x_0}+{y_0}=0$,
又${y_0}^2=4{x_0}$,所以$\frac{k}{4}{y^2}-y-\frac{k}{4}{y_0}^2+{y_0}=0$,
因为直线l与曲线C相切,所以$△=1-k(-\frac{k}{4}{y_0}^2+{y_0})=0$,解得$k=\frac{2}{y_0}$.
所以,直线l的方程为$4x-2{y_0}y+{y_0}^2=0$.
动圆M的半径即为点M(a,0)到直线l的距离$d=\frac{{|4a+{y_0}^2|}}{{\sqrt{16+4{y_0}^2}}}$.
当动圆M的面积最小时,即d最小,而当a>2时;$d=\frac{{|4a+{y_0}^2|}}{{\sqrt{16+4{y_0}^2}}}=\frac{{{y_0}^2+4a}}{{2\sqrt{{y_0}^2+4}}}$=$\frac{{{y_0}^2+4+4a-4}}{{2\sqrt{{y_0}^2+4}}}$=$\frac{{\sqrt{{y_0}^2+4}}}{2}+\frac{4a-4}{{2\sqrt{{y_0}^2+4}}}≥2\sqrt{a-1}$.
当且仅当${y_0}^2=4a-8$,即x0=a-2时取等号,
所以当动圆M的面积最小时,a-x0=2,
即当动圆M的面积最小时,M、P两点的横坐标之差为定值.
点评 本题考查轨迹方程的求法,直线与抛物线的位置关系的综合应用,考查转化思想以及计算能力.

| A. | ?x0>2,${2^{x_0}}-3≤0$ | B. | ?x≤2,2x-3>0 | C. | ?x>2,2x-3≤0 | D. | ?x0>2,${2^{x_0}}-3>0$ |
| A. | 否命题 | B. | 逆命题 | C. | 逆否命题 | D. | 否定形式 |
| A. | (0,+∞) | B. | (-∞,1) | C. | (-∞,2) | D. | (0,1) |
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{2}{3}$ |
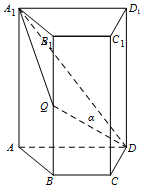 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,Q为BB1的中点,过A1,Q,D三点的平面记为α.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,Q为BB1的中点,过A1,Q,D三点的平面记为α.