题目内容
有以下命题:
①过空间一定点P与两异面直线a,b都相交的直线有且只有1条;
②平面α外的直线l与平面α内的无数条直线平行,则l∥α;
③异面直线a,b成角为θ,过空间一定点P作直线l与a,b成角都为
的直线有4条,则θ的取值范围为(
,
];
④空间四边形ABCD中,AB=CD=8,M,N分别是BD,AC的中点,若异面直线AB与CD所成角为60°,则MN=4.
其中正确命题有 .
①过空间一定点P与两异面直线a,b都相交的直线有且只有1条;
②平面α外的直线l与平面α内的无数条直线平行,则l∥α;
③异面直线a,b成角为θ,过空间一定点P作直线l与a,b成角都为
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
④空间四边形ABCD中,AB=CD=8,M,N分别是BD,AC的中点,若异面直线AB与CD所成角为60°,则MN=4.
其中正确命题有
考点:命题的真假判断与应用
专题:空间位置关系与距离,空间角
分析:本题①根据空间两条直线的位置关系,判断命题的真假,得到本题结论;②根据空间直线与平面的位置关系,判断命题的真假,得到本题结论;③根据空间三条直线的位置关系,判断命题的真假,得到本题结论;④根据异面直线所在的角的概念,构造三角形,计算得到MN的长,从而判断命题的真假,得到本题结论.
解答:
解:①过空间一定点P与两异面直线a,可以得到一个平面α,
当直线b∥平面α时,过点P与直线a,b都相交的直线不存在,
故命题①是错误的;
②由线面平行的判定,平面外一条直线与平面内一条直线平行,则该直线与平面平行.
平面α外的直线l与平面α内的无数条直线平行,显然有l∥α,、
故命题②正确;
③∵异面直线a,b成角为θ,过空间一定点P作直线l与a,b成角都为
的直线有4条,
∴过空间一定点P作直线a′∥a,b′∥b.
则直线a′与b′相交形成4个角,大小分别为θ,π-θ,θ,π-θ.
∵过空间一定点P作直线l与a,b成角都为
的直线有4条,
∴
,
∴
<θ<
,
又∵0<θ≤
∴θ的取值范围为(
,
];
故命题③正确;
④空间四边形ABCD中,AB=CD=8,M,N分别是BD,AC的中点,若异面直线AB与CD所成角为60°,
取BC中点P,连结PM、PN,
∴PM∥AB,PN∥BC,
PM=
BC=4,PN=
BC=4,
∵若异面直线AB与CD所成角为60°,
∴∠MPN=60°或∠MPN=120°,
∴MN=4或MN=4
.
故命题④不正确.
综上,正确的命题有②③.
故答案为:②③.
当直线b∥平面α时,过点P与直线a,b都相交的直线不存在,
故命题①是错误的;
②由线面平行的判定,平面外一条直线与平面内一条直线平行,则该直线与平面平行.
平面α外的直线l与平面α内的无数条直线平行,显然有l∥α,、
故命题②正确;
③∵异面直线a,b成角为θ,过空间一定点P作直线l与a,b成角都为
| π |
| 3 |
∴过空间一定点P作直线a′∥a,b′∥b.
则直线a′与b′相交形成4个角,大小分别为θ,π-θ,θ,π-θ.
∵过空间一定点P作直线l与a,b成角都为
| π |
| 3 |
∴
|
∴
| π |
| 3 |
| 2π |
| 3 |
又∵0<θ≤
| π |
| 2 |
∴θ的取值范围为(
| π |
| 3 |
| π |
| 2 |
故命题③正确;
④空间四边形ABCD中,AB=CD=8,M,N分别是BD,AC的中点,若异面直线AB与CD所成角为60°,
取BC中点P,连结PM、PN,
∴PM∥AB,PN∥BC,
PM=
| 1 |
| 2 |
| 1 |
| 2 |
∵若异面直线AB与CD所成角为60°,
∴∠MPN=60°或∠MPN=120°,
∴MN=4或MN=4
| 3 |
故命题④不正确.
综上,正确的命题有②③.
故答案为:②③.
点评:本题考查了命题真假的判断,还考查了空间直线与直线的位置关系、空间直线 与平面的位置关系,本题难度适中,属于中档题.

练习册系列答案
相关题目
设全集U=Z,P={1,2,3,4},Q={-1,2},则Q∩∁UP=( )
| A、{2} |
| B、{-1} |
| C、{-1,2} |
| D、{1,3,4} |
在空间直角坐标系中,A(-1,2,3),B(-2,-3,5),则|
|( )
| AB |
A、3
| ||
B、2
| ||
| C、30 | ||
D、
|
若直线a与平面α垂直,那么平面α与直线a平行的直线有( )
| A、0条 | B、0条或无数条 |
| C、无数条 | D、不确定 |
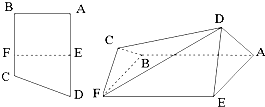 如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.
如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E,F分别为边AD和BC上的点,且EF∥AB,AD=2AE=2AB=4FC=4,将四边形EFCD沿EF折起成如图的位置,使AD=AE.