题目内容
18.连掷两次骰子得到的点数分别为m和n,记向量$\overrightarrow a=(m,n)$与向量$\overrightarrow b=(1,-1)$的夹角为θ,则θ为锐角的概率是$\frac{5}{12}$.分析 掷两次骰子分别得到的点数m,n,组成的向量(m,n)个数为36个,只需列举出满足条件的即可.
解答 解:后连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种
由于向量(m,n)与向量(1,-1)的夹角θ为锐角,∴(m,n)•(1,-1)>0,
即m>n,满足题意的情况如下:
当m=2时,n=1;
当m=3时,n=1,2;
当m=4时,n=1,2,3;
当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5;共有15种,
故所求事件的概率为:$\frac{15}{36}$=$\frac{5}{12}$,
故答案为:$\frac{5}{12}$.
点评 本题考查等可能事件的概率,得出m>n并正确列举是解决问题的关键,属基础题.

练习册系列答案
相关题目
8.已知函数g(x)的导函数g'(x)=ex,且g(0)g'(1)=e,(其中e为自然对数的底数).若?x∈(0,+∞),使得不等式$g(x)<\frac{x-m+3}{{\sqrt{x}}}$成立,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
6.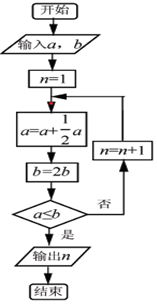 执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )
执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )
 执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )
执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
7.已知{an}为等差数列,Sn为其前n项和,若a1=2,S3=15,则a6=( )
| A. | 17 | B. | 14 | C. | 13 | D. | 3 |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线l:x-y+2=0平行,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{10}$ |
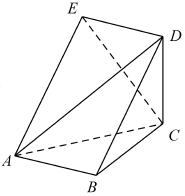 如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.
如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°,$CD=\sqrt{3}$.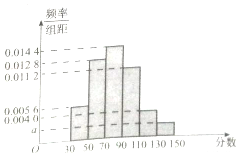 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)