题目内容
16.已知sin(α$-\frac{π}{8}$)=$\frac{4}{5}$,则cos(α+$\frac{3π}{8}$)=( )| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
分析 利用诱导公式化简要求的式子,可得结果.
解答 解:∵sin(α$-\frac{π}{8}$)=$\frac{4}{5}$,则cos(α+$\frac{3π}{8}$)=cos[$\frac{π}{2}$+(α-$\frac{π}{8}$)]=-sin(α-$\frac{π}{8}$)=-$\frac{4}{5}$,
故选:A.
点评 本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
7.已知函数f(x)=lnx,若4f′(x)+x≥a恒成立,则a的取值范围是( )
| A. | a≥4 | B. | a≤4 | C. | a≥2$\sqrt{2}$ | D. | a≤2$\sqrt{2}$ |
4.设集合A={0,1},B={x|(x+2)(x-1)<0,x∈Z},则A∪B=( )
| A. | {-2,-1,0,1} | B. | {-1,0,1} | C. | {0,1} | D. | {0} |
1.已知椭圆C1和双曲线C2焦点相同,且离心率互为倒数,F1,F2是它们的公共焦点,P是椭圆和双曲线在第一象限的交点,若∠F1PF2=60°,则椭圆C1的离心率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
8.已知函数g(x)的导函数g'(x)=ex,且g(0)g'(1)=e,(其中e为自然对数的底数).若?x∈(0,+∞),使得不等式$g(x)<\frac{x-m+3}{{\sqrt{x}}}$成立,则实数m的取值范围是( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (3,+∞) | D. | (-∞,4-e) |
5.等差数列{an}的前n项和是Sn,且a3=1,a5=4,则S13=( )
| A. | 39 | B. | 91 | C. | 48 | D. | 51 |
6.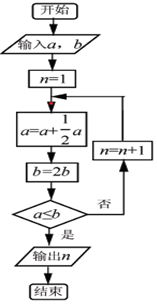 执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )
执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )
 执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )
执行如图所示的程序框图,若输入的a=16,b=4,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
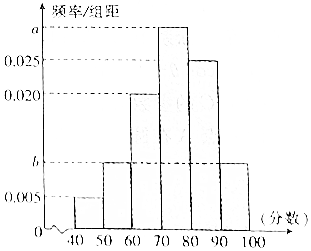 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.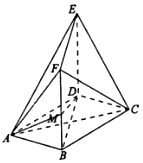 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF的中点.