题目内容
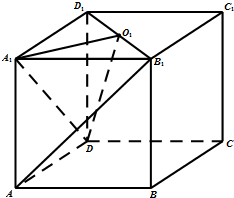 已知长方体ABCD-A1B1C1D1,点O1为B1D1的中点.
已知长方体ABCD-A1B1C1D1,点O1为B1D1的中点.(1)求证:AB1∥面A1O1D;
(2)若AB=
| 2 |
| 3 |
| BE |
| BB1 |
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结AD1交A1D于点G,由中位线定理得到O1G∥AB1,再由线面平行的判定定理即可证得;
(2)若在线段BB1上存在点E,使得A1C⊥AE,连结A1B交AE于点M,由线面垂直的性质和判定,得到AE⊥面A1BC,
根据三角形相似的判定,得到Rt△ABE∽Rt△A1AB,再由相似的性质得到存在点E有
=
.
(2)若在线段BB1上存在点E,使得A1C⊥AE,连结A1B交AE于点M,由线面垂直的性质和判定,得到AE⊥面A1BC,
根据三角形相似的判定,得到Rt△ABE∽Rt△A1AB,再由相似的性质得到存在点E有
| BE |
| BB1 |
| 4 |
| 9 |
解答:
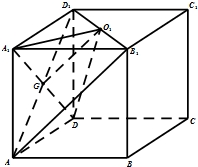 (1)证明:连结AD1交A1D于点G,
(1)证明:连结AD1交A1D于点G,
∴在△AB1D1中,G为AD1的中点,连结O1G,
O1为B1D1的中点,∴O1G∥AB1,
又O1G?面A1O1D且AB1?面A1O1D,
∴AB1∥面A1O1D;
(2)解:若在线段BB1上存在点E,使得A1C⊥AE,
连结A1B交AE于点M,又BC⊥面ABB1A1,且AE?面ABB1A1,
∴BC⊥AE,
又∵A1C∩BC=C,且A1C,BC?面A1BC,
∴AE⊥面A1BC,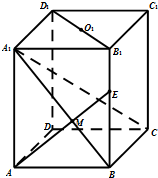
∵A1B?面A1BC,
∴AE⊥A1B,
在△AMB和△ABE中有:∠BAM+∠ABM=90°,∠BAM+∠BEA=90°,
∴∠ABM=∠BEA,同理:∠BAE=∠AA1B,
∴Rt△ABE∽Rt△A1AB,
∴
=
,∵AB=
AA1,∴BE=
AB=
BB1,
即在线段BB1上存在点E有
=
.
 (1)证明:连结AD1交A1D于点G,
(1)证明:连结AD1交A1D于点G,∴在△AB1D1中,G为AD1的中点,连结O1G,
O1为B1D1的中点,∴O1G∥AB1,
又O1G?面A1O1D且AB1?面A1O1D,
∴AB1∥面A1O1D;
(2)解:若在线段BB1上存在点E,使得A1C⊥AE,
连结A1B交AE于点M,又BC⊥面ABB1A1,且AE?面ABB1A1,
∴BC⊥AE,
又∵A1C∩BC=C,且A1C,BC?面A1BC,
∴AE⊥面A1BC,

∵A1B?面A1BC,
∴AE⊥A1B,
在△AMB和△ABE中有:∠BAM+∠ABM=90°,∠BAM+∠BEA=90°,
∴∠ABM=∠BEA,同理:∠BAE=∠AA1B,
∴Rt△ABE∽Rt△A1AB,
∴
| BE |
| AB |
| AB |
| AA1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
即在线段BB1上存在点E有
| BE |
| BB1 |
| 4 |
| 9 |
点评:本题考查直线与平面平行的判定定理,考查直线与平面垂直的判定与性质,考查存在性问题,注意运用假设,推结论,是一道中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
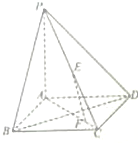 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E是PC中点,F为线段AC上一点.