题目内容
11．
某几何体的三视图如图所示（单位：cm），则该几何体的表面积是20+4$\sqrt{5}$cm2，体积是8cm3．
分析 由三视图作出原图形的直观图，结合图形求出它的表面积与体积．
解答 解：由三视图作出原图形如图所示，
原几何体为底面是边长为2cm、4cm的直角三角形，高为2cm的直三棱柱；
其表面积为S=2×$\frac{1}{2}$×2×4+4×2+2×2+2×$\sqrt{{4}^{2}{+2}^{2}}$=20+4$\sqrt{5}$cm2；
体积为V=$\frac{1}{2}$×4×2×2=8cm3．
故答案为：$20+4\sqrt{5}$，8．
点评 本题考查了三视图与体积、表面积的计算问题，是基础题目．
练习册系列答案
快捷英语周周练系列答案
相关题目
1．
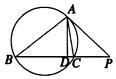如图所示，PA切圆于A，PA=8，直线PCB交圆于C，B，连接AB，AC，且PC=4，AD⊥BC于D，∠ABC=α，∠ACB=β，则$\frac{sinα}{sinβ}$的值等于（ ）
如图所示，PA切圆于A，PA=8，直线PCB交圆于C，B，连接AB，AC，且PC=4，AD⊥BC于D，∠ABC=α，∠ACB=β，则$\frac{sinα}{sinβ}$的值等于（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | 4 |
某几何体的三视图如图所不，则该几何体的表面积为22π+8．
16．设袋中有两个红球一个黑球，除颜色不同，其他均相同，现有放回的抽取，每次抽取一个，记下颜色后放回袋中，连续摸三次，X表示三次中红球被摸中的次数，每个小球被抽取的几率相同，每次抽取相对立，则方差D（X）=（ ）
| A． | 2 | B． | 1 | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
3．设α为钝角，且3sin2α=cosα，则sinα等于（ ）
| A． | $-\frac{1}{6}$ | B． | $\frac{1}{6}$ | C． | $\frac{{\sqrt{35}}}{6}$ | D． | $\frac{1}{3}$ |