题目内容
20.定义N*在上的函数f(x),对任意的正整数n1,n2,都有f(n1+n2)=1+f(n1)+f(n2),且f(1)=1,若对任意的正整数n,有${a_n}=f({2^n})+1$,则an=2n+1.分析 根据条件求出an=f(2n)+1的表达式,利用等比数列的定义即可证明{an}为等比数列,即可求出通项公式.
解答 解:令n1=n2=1,得f(2)=1+f(1)+f(1),
则f(2)=3,a1=f(2)+1=4,
令n1=n2=2,得f(4)=1+f(2)+f(2),则f(4)=7,a2=f(4)+1=8,
令n1=n2=2n,得f(2n+2n)=1+f(2n)+f(2n),
即f(2n+1)=1+2f(2n),
则f(2n+1)+1=2[1+f(2n)],an+1=2an
所以,数列{an}是等比数列,公比q=2,首项a1=4.
所以an=4×2n-1=2n+1,
故答案为:2n+1
点评 本题主要考查等比数列的判断和证明,综合性较强,考查学生的计算能力.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
10.下列命题正确的是( )
| A. | 若直线l上有无数个点不在平面α内,则l∥α | |
| B. | 若直线l与平面α有两个公共点,则直线l在平面内 | |
| C. | 若直线l与平面α相交,则l与平面α内的任意直线都是异面直线 | |
| D. | 平行于同一个平面的两条直线平行 |
 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是20+4$\sqrt{5}$cm2,体积是8cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的表面积是20+4$\sqrt{5}$cm2,体积是8cm3.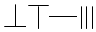 ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )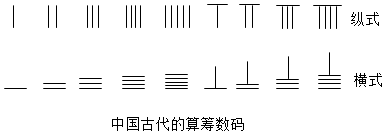
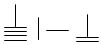
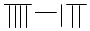

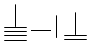
 已知一个几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的表面积为14+6$\sqrt{5}$+10π.
已知一个几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的表面积为14+6$\sqrt{5}$+10π.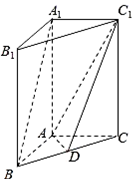 如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.