题目内容
19．已知直线a，b和平面α，若a∥b，且直线b在平面α上，则a与α的位置关系是a∥α或a?α．分析 利用已知条件真假判断直线与平面的位置关系即可．
解答 解：直线a，b和平面α，若a∥b，且直线b在平面α上，则a与α的位置关系是：a∥α或a?α．
如图：
故答案为：a∥α或a?α．
点评 本题考查直线与平面的位置关系的判断，基本知识的考查．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
9．已知$f（x）=-\frac{1}{2}{x^2}+6x-8lnx$在[m，m+1]上不单调，则实数m的取值范围是（ ）
| A． | （1，2） | B． | （3，4） | C． | （1，2]∪[3，4） | D． | （1，2）∪（3，4） |
10．下列命题正确的是（ ）
| A． | 若直线l上有无数个点不在平面α内，则l∥α | |
| B． | 若直线l与平面α有两个公共点，则直线l在平面内 | |
| C． | 若直线l与平面α相交，则l与平面α内的任意直线都是异面直线 | |
| D． | 平行于同一个平面的两条直线平行 |
14．已知函数f（x）=|x+1|-2|x-1|，则不等式f（x）＞1的解集为（ ）
| A． | （$\frac{2}{3}$，2） | B． | （$\frac{1}{3}$，2） | C． | （$\frac{2}{3}$，3） | D． | （$\frac{1}{3}$，3） |
4．设向量$\overrightarrow{a}$=（2，0），$\overrightarrow{b}$=（1，1），则下列结论中正确的是（ ）
| A． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B． | $\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$ | C． | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D． | （$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{b}$ |
某几何体的三视图如图所示（单位：cm），则该几何体的表面积是20+4$\sqrt{5}$cm2，体积是8cm3．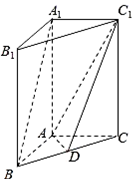
如图，在直三棱锥A1B1C1-ABC，AB⊥AC，AB=AC=2，AA1=4，点D是BC的中点．