题目内容
1.求证:cos($\frac{5k-1}{5}$π-θ)+cos($\frac{5k+1}{5}$π+θ)=(-1)k•2cos($\frac{π}{5}$+θ)(k∈Z)分析 根据三角函数的诱导公式,化简证明即可.
解答 证明:cos($\frac{5k-1}{5}$π-θ)+cos($\frac{5k+1}{5}$π+θ)
=cos(kπ-$\frac{π}{5}$-θ)+cos(kπ+$\frac{π}{5}$+θ)
=cos[kπ-($\frac{π}{5}$+θ)]+cos[kπ+($\frac{π}{5}$+θ)],
当k为偶数时,原式=cos[-($\frac{π}{5}$+θ)]+cos($\frac{π}{5}$+θ)=2cos($\frac{π}{5}$+θ);
当k为奇数时,原式=-cos($\frac{π}{5}$+θ)-cos($\frac{π}{5}$+θ)=-2cos($\frac{π}{5}$+θ);
综上,原式=(-1)k•2cos($\frac{π}{5}$+θ),(k∈Z),等式成立.
点评 本题考查了三角函数的诱导公式与分类讨论思想的应用问题,是基础题.

练习册系列答案
相关题目
16.张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:
(Ⅰ)求身高y关于年龄x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{1}-\overline{x})({y}_{1}-\overline{y})}{\sum_{i=1}^{n}({x}_{1}-\overline{x})^{2}}$,$\overline{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
(Ⅱ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{1}-\overline{x})({y}_{1}-\overline{y})}{\sum_{i=1}^{n}({x}_{1}-\overline{x})^{2}}$,$\overline{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
6.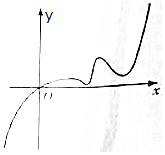 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是20+4$\sqrt{5}$cm2,体积是8cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的表面积是20+4$\sqrt{5}$cm2,体积是8cm3. 已知一个几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的表面积为14+6$\sqrt{5}$+10π.
已知一个几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的表面积为14+6$\sqrt{5}$+10π.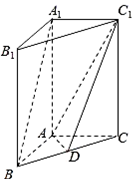 如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱锥A1B1C1-ABC,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.