题目内容
3.设α为钝角,且3sin2α=cosα,则sinα等于( )| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{{\sqrt{35}}}{6}$ | D. | $\frac{1}{3}$ |
分析 由已知可求sinα>0,cosα<0,利用二倍角的正弦函数公式即可计算求值得解.
解答 解:∵α为钝角,sinα>0,cosα<0,
∴3sin2α=cosα,可得:6sinαcosα=cosα,
∴sinα=$\frac{1}{6}$.
故选:B.
点评 本题主要考查了二倍角的正弦函数公式在三角函数化简求值中的应用,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
14.已知函数f(x)=|x+1|-2|x-1|,则不等式f(x)>1的解集为( )
| A. | ($\frac{2}{3}$,2) | B. | ($\frac{1}{3}$,2) | C. | ($\frac{2}{3}$,3) | D. | ($\frac{1}{3}$,3) |
18.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的一个焦点为F,该椭圆上有一点A,满足△OAF是等边三角形(O为坐标原点),则椭圆的离心率是( )
| A. | $\sqrt{3}-1$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{2}$ |
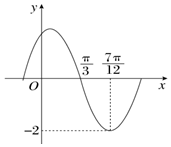 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,下列结论: 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是20+4$\sqrt{5}$cm2,体积是8cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的表面积是20+4$\sqrt{5}$cm2,体积是8cm3. 已知一个几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的表面积为14+6$\sqrt{5}$+10π.
已知一个几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的表面积为14+6$\sqrt{5}$+10π.