Question

16．设偶函数f（x）在（-∞，0）上是增函数，且f（-$\frac{1}{2}$）=0，则不等式$\frac{f（x）+f（-x）}{2x}＜0$的解集为（　　）

• A． （-$\frac{1}{2}$，0）∪（$\frac{1}{2}$，+∞）
• B． （-$\frac{1}{2}$，0）∪（0，$\frac{1}{2}$）
• C． （-∞，-$\frac{1}{2}$）∪（0，$\frac{1}{2}$）
• D． （-∞，-$\frac{1}{2}$）∪（$\frac{1}{2}$，+∞）

Answer 1

分析 根据函数奇偶性和单调性之间的关系将不等式进行转化即可．

解答 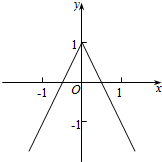解∵偶函数f（x）在（-∞，0）上是增函数，且f（-$\frac{1}{2}$）=0，
∴f（x）在（0，+∞）上为减函数，且f（$\frac{1}{2}$）=0，
则f（x）定义的图象为：
则∵f（x）是偶函数，
∴不等式$\frac{f（x）+f（-x）}{2x}＜0$等价为$\frac{2f（x）}{2x}$=$\frac{f（x）}{x}$＜0，
即x＞0时，f（x）＜0，即此时x＞$\frac{1}{2}$，
x＜0时，f（x）＞0，-$\frac{1}{2}$＜x＜0，
即不等式的解集为（-$\frac{1}{2}$，0）∪（$\frac{1}{2}$，+∞），
故选：A

点评 本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系作出函数的简单图象是解决本题的关键．