题目内容
1.已知1<x<m,a=logm2x,b=logmx2,c=logm(logmx),试比较a、b、c的大小.分析 由1<x<m得y=logmx 是一个增函数,比较b、c则是比较x2和logmx的大小,比较a、b,利用对数的性质把a、b作差比较大小,由此能比较a、b、c的大小.
解答 解:∵m>1,∴由1<x<m得,
y=logmx 是一个增函数,则我们要比较函数的大小只需比较自变量x的大小.
∴比较b、c则是比较x2和logmx的大小.
∵1<x<m,
∴0<logmx<1,x2>1;
通过y=logmx底数大于0的对数函数图象]可知,
logmx2>0,logm(logmx)<0,所以b>c,
∵a=logm2x,而 logmx>0,∴a>0,∴a>c,
比较a、b,利用对数的性质:logab2=2 logab,
把b化为2logmx,
可以把a、b作差比较大小,
b-a=2logmx-(logmx)2
=logmx(2-logmx),
∵2-logmx>0,0<logmx<1,
∴b>a,∴b>a>c.
点评 本题考查对数值大小的比较,是中档题,解题时要认真这题,注意对数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设偶函数f(x)在(-∞,0)上是增函数,且f(-$\frac{1}{2}$)=0,则不等式$\frac{f(x)+f(-x)}{2x}<0$的解集为( )
| A. | (-$\frac{1}{2}$,0)∪($\frac{1}{2}$,+∞) | B. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$)∪(0,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
13.对于函数f(x)=sinx+cosx,下列命题是真命题的是( )
| A. | ?x∈R,f(x)=f(x+π) | B. | .?x∈R,f(x)=$\frac{5}{3}$ | C. | .?x∈R,f(x)=-1 | D. | ?x∈R,f(x)<$\sqrt{2}$ |
11. 已知函数f(x)=ax3+bx2+cx+d(a≠0)的图象如图所示,则b的取值范围是( )
已知函数f(x)=ax3+bx2+cx+d(a≠0)的图象如图所示,则b的取值范围是( )
 已知函数f(x)=ax3+bx2+cx+d(a≠0)的图象如图所示,则b的取值范围是( )
已知函数f(x)=ax3+bx2+cx+d(a≠0)的图象如图所示,则b的取值范围是( )| A. | (-∞,0) | B. | (0,1) | C. | (1,2) | D. | (2,+∞) |
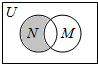 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.