题目内容
8．已知点M（4，-1），点P是直线l：y=2x+3上的任一点，则|PM|最小值为$\frac{{12\sqrt{5}}}{5}$．分析 可得|PM|最小值即为点M到直线l的距离，由点到直线的距离公式计算可得．
解答 解：由题意可得|PM|最小值即为点M到直线l的距离，
由距离公式可得d=$\frac{|2×4-（-1）+3|}{\sqrt{{2}^{2}+（-1）^{2}}}$=$\frac{{12\sqrt{5}}}{5}$，
故答案为：$\frac{{12\sqrt{5}}}{5}$．
点评 本题考查点到直线的距离公式，属基础题．
练习册系列答案
相关题目
13．已知x，y的取值如表所示，且线性回归方程为$\widehat{y}$=bx+$\frac{13}{2}$，则b=（ ）
| x | 2 | 3 | 4 |
| y | 6 | 4 | 5 |
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $-\frac{1}{3}$ | D． | $-\frac{1}{2}$ |
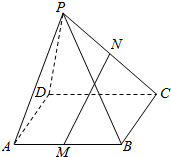如图，在四棱锥P-ABCD中，四边形ABCD是平行四边形，三角形ADP中AD=AP=5，PD=6，M、N分别是AB，PC的中点．
如图，已知PA⊥平面ABC，AC⊥AB，AP=BC，∠CBA=30°，D、E分别是BC、AP的中点．则异面直线AC与DE所成角的正切值为$\sqrt{7}$．
18．已知集合A={x|x2-3x+2＞0}，集合B={y|y=2cosx+1}，则（∁RA）∩B=（ ）
| A． | （-∞，-1）∪（2，+∞） | B． | [1，2] | C． | [-1，1）∪（2，3] | D． | [-1，3] |