题目内容
19.三角形△ABC三边a,b,c满足${a^2}+\frac{1}{2}ab={c^2}-{b^2}$,则角C的值为$π-arccos\frac{1}{4}$.(结果用反三角函数值表示).分析 由已知及余弦定理可求cosC=-$\frac{1}{4}$,结合范围C∈(0,π),可知C为钝角,即可用反三角函数值表示C的值.
解答 解:∵${a^2}+\frac{1}{2}ab={c^2}-{b^2}$,即:${a}^{2}+{b}^{2}-{c}^{2}=-\frac{1}{2}ab$,
∴由余弦定理可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{-\frac{1}{2}ab}{2ab}$=-$\frac{1}{4}$,
∴由C∈(0,π),可知C为钝角,C=$π-arccos\frac{1}{4}$.
故答案为:$π-arccos\frac{1}{4}$.
点评 本题主要考查了余弦定理在解三角形中的应用,考查了反三角函数表示角,属于基础题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
10.执行如图所示的程序框图,则输出的结果是( )
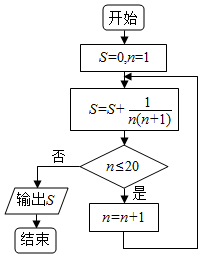

| A. | $\frac{22}{23}$ | B. | $\frac{21}{22}$ | C. | $\frac{20}{21}$ | D. | $\frac{19}{20}$ |
11.下列问题中,应采用哪种抽样方法( )
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
| A. | 分层抽样、分层抽样、抽签法、系统抽样 | |
| B. | 分层抽样、分层抽样、随机数法、系统抽样 | |
| C. | 抽签法、分层抽样、随机数法、系统抽样 | |
| D. | 抽签法、分层抽样、系统抽样、随机数法 |