题目内容
17. 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点.则异面直线AC与DE所成角的正切值为$\sqrt{7}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点.则异面直线AC与DE所成角的正切值为$\sqrt{7}$.
分析 取AB中点F,连接DF,EF,则AC∥DF,∠EDF就是异面直线AC与PB所成的角.由此能求出异面直线AC与DE所成角的正切值.
解答 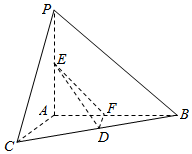 解:取AB中点F,连接DF,EF,则AC∥DF,
解:取AB中点F,连接DF,EF,则AC∥DF,
∴∠EDF就是异面直线AC与PB所成的角.
设AP=BC=2,由已知,AC=EA=AD=1,AB=$\sqrt{3}$,PB=$\sqrt{7}$,
∵AC⊥EF,∴DF⊥EF.
在Rt△EFD中,DF=$\frac{1}{2}$,ED=2,cos$∠EDF=\frac{\sqrt{2}}{4}$.
∴sin$∠EDF=\sqrt{1-\frac{2}{16}}$=$\frac{\sqrt{14}}{4}$,tan∠EDF=$\frac{sin∠EDF}{cos∠EDF}$=$\frac{\frac{\sqrt{14}}{4}}{\frac{\sqrt{2}}{4}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.△ABC的内角A、B、C的对边分别为a,b,c,且a:b:c=$\sqrt{13}$:4:3,设$\overrightarrow{m}$=$\overrightarrow{AB}$cosA,$\overrightarrow{n}$=$\overrightarrow{AC}$sinA,又△ABC的面积为S,则$\overrightarrow{m}$•$\overrightarrow{n}$=( )
| A. | $\frac{\sqrt{13}}{2}$S | B. | $\frac{3}{2}$S | C. | S | D. | $\frac{1}{2}$S |