题目内容
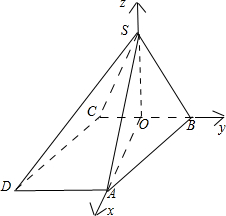
 如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2.
如图所示,四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,∠ABC=45°,AB=SA=SB=2.(1)证明:SA⊥BC;
(2)求直线SB与平面SDA所成的角的大小.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:平面向量及应用
分析:(1)由于侧面SBC⊥底面ABCD,所以根据面面垂直的性质定理,可以过S作BC的垂线,若设垂足为O,连接OA,则SO⊥OA,所以很容易证明Rt△SOB⊥Rt△SOA,从而会得到∠BOA=90°,从而证明BC⊥平面SOA,∴SA⊥BC.
(2)要求直线SB与平面SDA所成的角,要先找到这个角,直接找不好找,这时候可以利用向量的办法,设过B作平面SDA的垂线,垂足设为E,然后根据向量的办法,找到E的坐标即可.找到坐标之后,直线SB与平面SDA所成的角就等于向量
和
所成角,利用向量便能求出这个角.
(2)要求直线SB与平面SDA所成的角,要先找到这个角,直接找不好找,这时候可以利用向量的办法,设过B作平面SDA的垂线,垂足设为E,然后根据向量的办法,找到E的坐标即可.找到坐标之后,直线SB与平面SDA所成的角就等于向量
| SB |
| SE |
解答:
(1)证明:作SO⊥BC,垂足是O,连接AO,SO;
∵侧面SBC⊥底面ABCD,侧面SBC∩底面ABCD=BC;
∴SO⊥底面ABCD;
又∵OA?底面ABCD;
∴SO⊥OA,SO⊥OB;
又 SA=SB
∴OA=OB;
又∠ABC=45°
∴OA⊥OB;
∴BC⊥OA
又∵BC⊥SO,SO∩AO=O
∴BC⊥平面SOA;
又∵SA?平面SOA
∴SA⊥BC.
(2)以OA、OB、OS为x、y、z轴建立如图所示空间直角坐标系;
∵AB=2,∠ABC=45°
∴OB=
×2=
,OA=
,又SB=2,∴OS=
;
∴能确定以下几点坐标:
A(
,0,0),S(0,0,
),B(0,
,0),设D(
,a,0),
若过B作平面ADS的垂线,设垂足为E(x0,y0,z0),则:
=(0,a,0),
=(-
,0,
),
=(x0,y0-
,z0),
=(x0-
,y0,z0)则:
•
=0,
•
=0,∴带入坐标得:a(y0-
)=0,-
x0+
z0=0,∴y0=
,x0=z0;
又E在平面ADS上,∴存在实数λ,μ使得
=λ
+μ
,带入坐标得(z0-
,
,z0)=λ(0,a,0)+μ(-
,0,
);
∴
,解得z0=
,∴x0=
,∴E(
,
,
),∴
=(0,
,-
),
=(
,
,-
);
通过前面知:向量
和
所成的角就是直线SB与平面SDA所成的角,设这个角为θ,则:
cosθ=
═
=
,∴θ=30°.

∵侧面SBC⊥底面ABCD,侧面SBC∩底面ABCD=BC;
∴SO⊥底面ABCD;
又∵OA?底面ABCD;
∴SO⊥OA,SO⊥OB;
又 SA=SB
∴OA=OB;
又∠ABC=45°
∴OA⊥OB;
∴BC⊥OA
又∵BC⊥SO,SO∩AO=O
∴BC⊥平面SOA;
又∵SA?平面SOA
∴SA⊥BC.
(2)以OA、OB、OS为x、y、z轴建立如图所示空间直角坐标系;
∵AB=2,∠ABC=45°
∴OB=
| ||
| 2 |
| 2 |
| 2 |
| 2 |
∴能确定以下几点坐标:
A(
| 2 |
| 2 |
| 2 |
| 2 |
若过B作平面ADS的垂线,设垂足为E(x0,y0,z0),则:
| AD |
| AS |
| 2 |
| 2 |
| BE |
| 2 |
| AE |
| 2 |
| BE |
| AS |
| BE |
| AD |
| 2 |
| 2 |
| 2 |
| 2 |
又E在平面ADS上,∴存在实数λ,μ使得
| AE |
| AD |
| AS |
| 2 |
| 2 |
| 2 |
| 2 |
∴
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| SB |
| 2 |
| 2 |
| SE |
| ||
| 2 |
| 2 |
| ||
| 2 |
通过前面知:向量
| SB |
| SE |
cosθ=
| ||||
|
|
| 2+1 | ||
2×
|
| ||
| 2 |
点评:第一问告诉我们,要证明线线垂直,可通过证明线面垂直得到.第二问的求解过程,便是利用向量方法求线面角的方法,需要掌握,并且利用向量的方法还可以求其它的夹角问题.考查的知识点为:面面垂直的性质定理,线面垂直的判定定理,向量的数量积,平面向量基本定理,向量夹角.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 如图所示的曲线C由曲线C1:
如图所示的曲线C由曲线C1: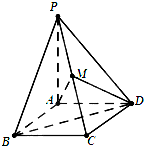 在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=1,点M是棱PC的中点.
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=1,点M是棱PC的中点. 某次游园的一项活动中,设置了两个中奖方案:
某次游园的一项活动中,设置了两个中奖方案: