题目内容
7.三角形ABC中,AB=2,AC=3,以BC为边向形外作等边三角形BCD,问角A为何值时,四边形ABCD面积最大?并求出最大值.分析 利用余弦定理,求出BC,表示出四边形ABCD面积,利用辅助角公式化简,即可得出结论.
解答 解:设∠BAC=x,则根据余弦定理BC2=22+32-2×2×3×cosx=13-12cosx
于是S四边形ABCD=$\frac{1}{2}×2×3×$sinx+$\frac{\sqrt{3}}{4}$(13-12cosx)=3sinx-3$\sqrt{3}$cosx+$\frac{13\sqrt{3}}{4}$=6sin(x-60°)+$\frac{13\sqrt{3}}{4}$.
所以当x为150°时最大,最大值为6+$\frac{13\sqrt{3}}{4}$.
点评 本题考查余弦定理,考查四边形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.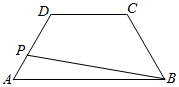 如图,在等腰梯形ABCD中,AB=8,BC=4,CD=4,点P在线段AD上运动,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是( )
如图,在等腰梯形ABCD中,AB=8,BC=4,CD=4,点P在线段AD上运动,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是( )
 如图,在等腰梯形ABCD中,AB=8,BC=4,CD=4,点P在线段AD上运动,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是( )
如图,在等腰梯形ABCD中,AB=8,BC=4,CD=4,点P在线段AD上运动,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是( )| A. | [6,4+4$\sqrt{3}$] | B. | [4$\sqrt{2}$,8] | C. | [4$\sqrt{3}$,8] | D. | [6,12] |