题目内容
17.已知a,b∈R,且a2+b2≤9,求|a|-|b|的最大值.分析 根据绝对值不等式的性质求出其最大值即可.
解答 解:|a|-|b|≤|a-b|≤$\sqrt{{a}^{2}{+b}^{2}}$≤$\sqrt{9}$=3,
故|a|-|b|的最大值是3.
点评 本题考查了绝对值不等式的性质,是一道基础题.

练习册系列答案
相关题目
12.若函数f(x)=sinωx+cosωx(ω>0)的图象相邻两条对称轴之间的距离为3,则ω值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
2.若a、b表示两条直线,α表示平面,下列命题中的真命题为( )
| A. | 若a⊥α,a⊥b,则b∥α | B. | 若a∥α,a⊥b,则b⊥α | C. | 若a⊥α,b⊆α,则a⊥b | D. | 若a∥α,b∥α,则a∥b |
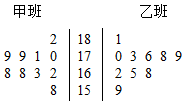 从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.
从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.