题目内容
16.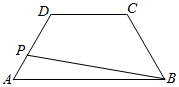 如图,在等腰梯形ABCD中,AB=8,BC=4,CD=4,点P在线段AD上运动,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是( )
如图,在等腰梯形ABCD中,AB=8,BC=4,CD=4,点P在线段AD上运动,则|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的取值范围是( )| A. | [6,4+4$\sqrt{3}$] | B. | [4$\sqrt{2}$,8] | C. | [4$\sqrt{3}$,8] | D. | [6,12] |
分析 可过D作AB的垂线,且垂足为E,这样可分别以EB,ED为x轴,y轴,建立平面直角坐标系,根据条件即可求出A,B,D的坐标,从而可以得出直线AD的方程为$y=\sqrt{3}x+2\sqrt{3}$,从而可设$P(x,\sqrt{3}x+2\sqrt{3})$,且-2≤x≤0,从而可以求出向量$\overrightarrow{PA}+\overrightarrow{PB}$的坐标,从而得出$(\overrightarrow{PA}+\overrightarrow{PB})^{2}=16({x}^{2}+2x+4)$,而配方即可求出函数y=16(x2+2x+4)在[-2,0]上的值域,即得出$(\overrightarrow{PA}+\overrightarrow{PB})^{2}$的取值范围,从而得出$|\overrightarrow{PA}+\overrightarrow{PB}|$的取值范围.
解答 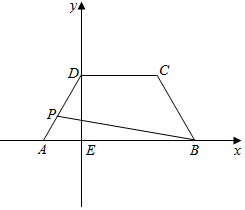 解:如图,过D作AB的垂线,垂足为E,分别以EB,ED为x,y轴,建立平面直角坐标系;
解:如图,过D作AB的垂线,垂足为E,分别以EB,ED为x,y轴,建立平面直角坐标系;
根据条件可得,AE=2,EB=6,DE=$2\sqrt{3}$;
∴$A(-2,0),B(6,0),D(0,2\sqrt{3})$;
∴直线AD方程为:$y=\sqrt{3}x+2\sqrt{3}$;
∴设$P(x,\sqrt{3}x+2\sqrt{3})$,(-2≤x≤0);
∴$\overrightarrow{PA}=(-2-x,-\sqrt{3}x-2\sqrt{3})$,$\overrightarrow{PB}=(6-x,-\sqrt{3}x-2\sqrt{3})$;
∴$\overrightarrow{PA}+\overrightarrow{PB}=(4-2x,-2\sqrt{3}-4\sqrt{3})$;
∴$(\overrightarrow{PA}+\overrightarrow{PB})^{2}=(4-2x)^{2}+(-2\sqrt{3}x-4\sqrt{3})^{2}$
=16(x2+2x+4)
=16(x+1)2+48;
∵-2≤x≤0;
∴48≤16(x+1)2+48≤64;
即$48≤(\overrightarrow{PA}+\overrightarrow{PB})^{2}≤64$;
∴$4\sqrt{3}≤|\overrightarrow{PA}+\overrightarrow{PB}|≤8$;
∴$|\overrightarrow{PA}+\overrightarrow{PB}|$的范围为$[4\sqrt{3},8]$.
故选:C.
点评 考查通过建立平面直角坐标系,利用坐标解决向量问题的方法,能根据条件求平面上点的坐标,根据点的坐标可求向量的坐标,直线的点斜式方程,以及直线上点的坐标的设法,向量坐标的加法运算,以及向量数量积的坐标运算,配方求二次函数在闭区间上的值域的方法.

 阅读快车系列答案
阅读快车系列答案| A. | x2-$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-y2=1 | C. | $\frac{{x}^{2}}{\sqrt{3}}$-y2=1 | D. | x2-$\frac{{y}^{2}}{9}$=1 |