题目内容
19．数列{an}满足an+1-an=an-an-1（n≥2，n∈N），a3=11，Sn为其前n项和，则S5=（ ）| A． | 45 | B． | 50 | C． | 55 | D． | 60 |
分析 先判断数列为等差数列，再根据性质和前n项和公式计算即可．
解答 解：数列{an}满足an+1-an=an-an-1（n≥2，n∈N），
∴数列{an}为等差数列，
∴S5=$\frac{5（{a}_{1}+{a}_{5}）}{2}$=5a3=55，
故选：C
点评 本题考查了等差数列的定义和性质以及前n项和公式，属于基础题．
练习册系列答案
寒假学与练系列答案
相关题目
4．某化肥厂用三种原料生产甲乙两种肥料，生产1吨甲种肥料和生产1吨乙种肥料所需三种原料的吨数如右表所示：已知生产1吨甲种肥料产生的利润2万元，生产1吨乙种肥料产生的利润为3万元，现有A种原料20吨，B种原料36吨，C种原料32吨，在此基础上安排生产，则生产甲乙两种肥料的利润之和的最大值为（ ）
 | A | B | C |
| 甲 | 2 | 4 | 2 |
| 乙 | 4 | 4 | 8 |
| A． | 17万元 | B． | 18万元 | C． | 19万元 | D． | 20万元 |
11．2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示：
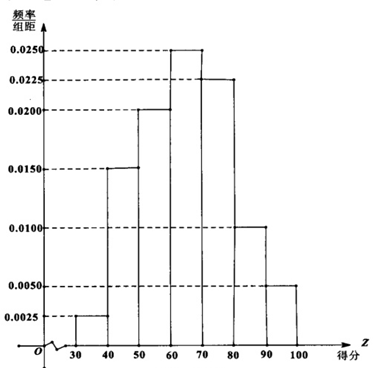
（1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
（2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案：
①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
②每次赠送的随机话费和对应概率如下：
现有一位市民要参加此次问卷调查，记X（单位：元）为该市民参加问卷调查获赠的话费，求X的分布列．
附：$\sqrt{210}$≈14.5
若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．
（1）由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N（μ，210），μ近似为这1000人得分的平均值（同一组数据用该区间的中点值作代表），利用该正态分布，求P（50.5＜Z＜94）．
（2）在（1）的条件下，有关部门为此次参加问卷调查的市民制定如下奖励方案：
①得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
②每次赠送的随机话费和对应概率如下：
| 赠送话费（单位：元） | 10 | 20 |
| 概率 | $\frac{2}{3}$ | $\frac{1}{3}$ |
附：$\sqrt{210}$≈14.5
若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．
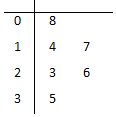据统计，目前微信用户已达10亿，2016年，诸多传统企业大佬纷纷尝试进入微商渠道，让这个行业不断地走向正规化、规范化．2017年3月25日，第五届中国微商博览会在山东济南舜耕国际会展中心召开，力争为中国微商产业转型升级．某品牌饮料公司对微商销售情况进行中期调研，从某地区随机抽取6家微商一周的销售金额（单位：百元）的茎叶图如图所示，其中茎为十位数，叶为个位数．