题目内容
已知常数a>0,函数f(x)=ln(1+x)-
.
(1)讨论f(x)的单调性;
(2)若f(x)有两个极值点x1,x2,求f(x1)+f(x2),并注明a的取值范围;
(3)若f′(x)是f(x)的导函数,f′(x)>0,求a的取值范围.
| 2ax |
| x+2 |
(1)讨论f(x)的单调性;
(2)若f(x)有两个极值点x1,x2,求f(x1)+f(x2),并注明a的取值范围;
(3)若f′(x)是f(x)的导函数,f′(x)>0,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=
-
=
(x2+(4-4a)x+4-4a),令g(x)=x2+(4-4a)x+4-4a,讨论g(x)的正负推导f′(x)的正负,从而推导f(x)的单调性;
(2)结合(1)可得f(x1)+f(x2)=f(2a-2-2
)+f(2a-2+2
),代入化简即可.
(3)由(1)可直接写出答案.
| 1 |
| 1+x |
| 4a |
| (x+2)2 |
| 1 |
| (x+1)(x+2)2 |
(2)结合(1)可得f(x1)+f(x2)=f(2a-2-2
| a(a-1) |
| a(a-1) |
(3)由(1)可直接写出答案.
解答:
解:(1)∵f(x)=ln(1+x)-
,
∴f′(x)=
-
=
(x2+(4-4a)x+4-4a);
①令g(x)=x2+(4-4a)x+4-4a,
当△=(4-4a)(4-4a)-4(4-4a)
=(4-4a)(4-4a-4)
=-16a(1-a)≤0,
即0<a≤1时,g(x)≥0;
故f′(x)≥0,
故f(x)在定义域(-1,+∞)上是增函数;
②当a>1时,4-4a<0,故x2+(4-4a)x+4-4a=0有两个根,
且一正一负,
又∵g(-1)=1>0,
∴x2+(4-4a)x+4-4a=0的两个根都大于-1;
x2+(4-4a)x+4-4a=0的两个根为
x1=2a-2-2
,x2=2a-2+2
;
故当x∈(-1,2a-2-2
),(2a-2+2
,+∞)时,
f′(x)>0,f(x)是增函数;
当x∈(2a-2-2
,2a-2+2
)时,f′(x)<0,
f(x)是减函数;
(2)由(1)知,当a>1时,(x)有两个极值点x1,x2,
f(x1)+f(x2)=f(2a-2-2
)+f(2a-2+2
)
=ln(1+2a-2-2
)+ln(1+2a-2+2
)
-4a+
+
=0-4a+4a=0,
故f(x1)+f(x2)=0,a>1;
(3)由(1)知,当0<a<1时,f′(x)>0.
故a的取值范围为(0,1).
| 2ax |
| x+2 |
∴f′(x)=
| 1 |
| 1+x |
| 4a |
| (x+2)2 |
=
| 1 |
| (x+1)(x+2)2 |
①令g(x)=x2+(4-4a)x+4-4a,
当△=(4-4a)(4-4a)-4(4-4a)
=(4-4a)(4-4a-4)
=-16a(1-a)≤0,
即0<a≤1时,g(x)≥0;
故f′(x)≥0,
故f(x)在定义域(-1,+∞)上是增函数;
②当a>1时,4-4a<0,故x2+(4-4a)x+4-4a=0有两个根,
且一正一负,
又∵g(-1)=1>0,
∴x2+(4-4a)x+4-4a=0的两个根都大于-1;
x2+(4-4a)x+4-4a=0的两个根为
x1=2a-2-2
| a(a-1) |
| a(a-1) |
故当x∈(-1,2a-2-2
| a(a-1) |
| a(a-1) |
f′(x)>0,f(x)是增函数;
当x∈(2a-2-2
| a(a-1) |
| a(a-1) |
f(x)是减函数;
(2)由(1)知,当a>1时,(x)有两个极值点x1,x2,
f(x1)+f(x2)=f(2a-2-2
| a(a-1) |
| a(a-1) |
=ln(1+2a-2-2
| a(a-1) |
| a(a-1) |
-4a+
| 4a | ||
2a-2
|
| 4a | ||
2a+2
|
=0-4a+4a=0,
故f(x1)+f(x2)=0,a>1;
(3)由(1)知,当0<a<1时,f′(x)>0.
故a的取值范围为(0,1).
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
相关题目
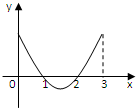 函数f(x)定义域为[0,3],导函数f′(x)在[0,3]内图象如图所示,则函数f(x)在[0,3]的单调递减区间为( )
函数f(x)定义域为[0,3],导函数f′(x)在[0,3]内图象如图所示,则函数f(x)在[0,3]的单调递减区间为( )| A、[0,1] |
| B、[1,2] |
| C、[2,3] |
| D、[0,2] |