题目内容
在空间直角坐标系中,若一条直线与三条坐标面所成的角都相等,则这个角的余弦值为 .
考点:直线与平面所成的角
专题:空间角
分析:设直线的方向向量为(x,y,z),三个坐标面的法向量分别为:(1,0,0),(0,1,0),(0,0,1),利用向量的数量积与夹角的关系求夹角的正弦值即可.
解答:
解:设直线的方向向量为(x,y,z),三个坐标面的法向量分别为:(1,0,0),(0,1,0),(0,0,1),
因为直线与三条坐标面所成的角都相等,所以(x,y,z)(1,0,0)=(x,y,z)(0,1,0)=(x,y,z)(0,0,1),
所以x=y=z,取x=1,则直线的一个方向向量为(1,1,1),
因为一条直线与三条坐标面所成的角都相等,则这个角的余弦值为直线方向向量与坐标平面的法向量夹角的正弦值,
而直线方向向量与坐标平面的法向量夹角的余弦值为
,所以直线方向向量与坐标平面的法向量夹角的正弦值为
;
故答案为:
.
因为直线与三条坐标面所成的角都相等,所以(x,y,z)(1,0,0)=(x,y,z)(0,1,0)=(x,y,z)(0,0,1),
所以x=y=z,取x=1,则直线的一个方向向量为(1,1,1),
因为一条直线与三条坐标面所成的角都相等,则这个角的余弦值为直线方向向量与坐标平面的法向量夹角的正弦值,
而直线方向向量与坐标平面的法向量夹角的余弦值为
| 1 | ||
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查了线面角的余弦值求法,关键是将问题转化为直线的方向向量与坐标平面的法向量的夹角问题.

练习册系列答案
相关题目
已知半径为3的圆C的圆心与点P(-2,1)关于直线x-y+1=0对称,则圆C的标准方程为( )
| A、(x+1)2+(y-1)2=9 |
| B、(x-1)2+(y-1)2=81 |
| C、x2+y2=9 |
| D、x2+(y+1)2=9 |
在同一坐标系中,函数y=ax+a与y=ax的图象大致是( )
A、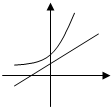 |
B、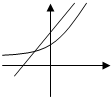 |
C、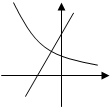 |
D、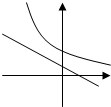 |
在△ABC中,sin2A+sin2B+sin2C=2
sinAsinBsinC,则△ABC的形状是( )
| 3 |
| A、直角三角形 |
| B、等腰直角三角形 |
| C、钝角三角形 |
| D、正三角形 |
已知集合M={x|x2-2x≤0},N={x|
≤0},U=R,则图中阴影部分表示的集合是( )
| 3+x |
| 1-x |

| A、(-∞,0)∪(1,+∞) |
| B、(-∞,-3]∪(2,+∞) |
| C、(-∞,-3)∪(2,+∞) |
| D、(-∞,0]∪[2,+∞) |
若a是从区间[-2,2]任取的一个数,b是从区间[-2,2]任取的一个数,则关于x的一元二次方程x2+2ax-(b2-1)=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|