题目内容
已知空间四边形ABCD的4条边和两条对角线相等，E为AD中点求EC与平面BCD所成角的正切值 ．
考点：直线与平面所成的角
专题：空间位置关系与距离
分析：作DF⊥BC，交BC于F，作AO⊥平在BDC，交DF于O，作EP⊥平面BDC，交DF于P，连结EC，CP，则∠PCE是CE与平面DBC所成角，由此能求出CE与平面DBC所成角的正弦值．
解答：
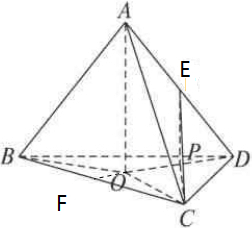解：作DE⊥BC，交BC于F，作AO⊥平在BDC，交DF于O，
作PE⊥平面BDC，交DF于P，连结EC，CP，
则∠PCE是CQE平面DBC所成角，
设正四面体ABCD的棱长为2，
则DF=EC=DF=
=
，
DO=
DF=
，DP=
，
AO=
=
，PE=
AO=
，
则sin∠PCE=
=
，
cos∠PCE=
，
tan∠PCE=
．
故答案为；
．
解：作DE⊥BC，交BC于F，作AO⊥平在BDC，交DF于O，作PE⊥平面BDC，交DF于P，连结EC，CP，
则∠PCE是CQE平面DBC所成角，
设正四面体ABCD的棱长为2，
则DF=EC=DF=
| 22-12 |
| 3 |
DO=
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
AO=
4-
|
2
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
则sin∠PCE=
| PE |
| EC |
| ||
| 3 |
cos∠PCE=
| ||
| 3 |
tan∠PCE=
| ||
| 7 |
故答案为；
| ||
| 7 |
点评：本题考查直线与平面所成角的正弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
教材全解字词句篇系列答案
相关题目
在同一坐标系中，函数y=ax+a与y=ax的图象大致是（ ）
A、 |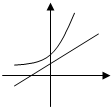
B、 |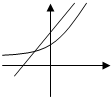
C、 |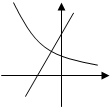
D、 |
已知集合M={x|x2-2x≤0}，N={x|
≤0}，U=R，则图中阴影部分表示的集合是（ ）
| 3+x |
| 1-x |
| A、（-∞，0）∪（1，+∞） |
| B、（-∞，-3]∪（2，+∞） |
| C、（-∞，-3）∪（2，+∞） |
| D、（-∞，0]∪[2，+∞） |
若a是从区间[-2，2]任取的一个数，b是从区间[-2，2]任取的一个数，则关于x的一元二次方程x2+2ax-（b2-1）=0有实根的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|