题目内容
设数列{an}的前n项和为Sn,已知a1=a,an+1=Sn+3n,n∈N*.
(1)记bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
(1)记bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
考点:数列递推式,数列的函数特性
专题:等差数列与等比数列
分析:(1)由已知得Sn+1=2Sn+3n,由此得Sn+1-3n+1=2(Sn-3n),从而能求出数列{bn}的通项公式.
(2)由Sn=3n+(a-3)•2n-1,n∈N*,得an=Sn-Sn-1=2×3n-1+(a-3)•2n-2,从而an+1-an=2n-2[12•(
)n-2+a-3],当n≥2时,an+1≥an,等价于12•(
)n-2+a-3≥0,由此能求出a的取值范围.
(2)由Sn=3n+(a-3)•2n-1,n∈N*,得an=Sn-Sn-1=2×3n-1+(a-3)•2n-2,从而an+1-an=2n-2[12•(
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)依题意,Sn+1-Sn=an+1=Sn+3n,
∴Sn+1=2Sn+3n,
由此得Sn+1-3n+1=2(Sn-3n),
又S1-3=a-3,
∴{Sn-3n}是首项为a-3,公比为2的等比数列,
∴所求通项公式为bn=Sn-3n=(a-3)•2n-1,n∈N*.
(2)由(1)知Sn=3n+(a-3)•2n-1,n∈N*,
于是,当n≥2时,
an=Sn-Sn-1=3n+(a-3)×2n-1-3n-1-(a-3)×2n-2
=2×3n-1+(a-3)•2n-2,
an+1-an=4×3n-1+(a-3)•2n-2
=2n-2[12•(
)n-2+a-3],
当n≥2时,an+1≥an,等价于12•(
)n-2+a-3≥0,
解得a≥-9.
又a2=a1+3>a1,
∴a的取值范围是[-9,+∞).
∴Sn+1=2Sn+3n,
由此得Sn+1-3n+1=2(Sn-3n),
又S1-3=a-3,
∴{Sn-3n}是首项为a-3,公比为2的等比数列,
∴所求通项公式为bn=Sn-3n=(a-3)•2n-1,n∈N*.
(2)由(1)知Sn=3n+(a-3)•2n-1,n∈N*,
于是,当n≥2时,
an=Sn-Sn-1=3n+(a-3)×2n-1-3n-1-(a-3)×2n-2
=2×3n-1+(a-3)•2n-2,
an+1-an=4×3n-1+(a-3)•2n-2
=2n-2[12•(
| 3 |
| 2 |
当n≥2时,an+1≥an,等价于12•(
| 3 |
| 2 |
解得a≥-9.
又a2=a1+3>a1,
∴a的取值范围是[-9,+∞).
点评:本题考查数列的通项公式的求法,考查实数的取值范围的求法,是中档题,解题时要注意构造法的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
已知i为虚数单位复数z=
对应的点位于第四象限,则实数a的取值范围是( )
| 1+ai |
| 1+i |
| A、(-1,+∞) |
| B、(-∞,1) |
| C、(-1,1) |
| D、(-1,0) |
设数列{an}的前n项和为Sn,4Sn=an2+2an-3,且a1,a2,a3,a4,a5成等比数列,当n≥5时,an>0.
(1)求证:当n≥5时 {an}成等差数列;
(2)求{an}的前n项和Sn.
(1)求证:当n≥5时 {an}成等差数列;
(2)求{an}的前n项和Sn.
在同一坐标系中,函数y=ax+a与y=ax的图象大致是( )
A、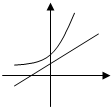 |
B、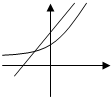 |
C、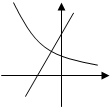 |
D、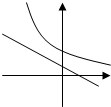 |
在△ABC中,sin2A+sin2B+sin2C=2
sinAsinBsinC,则△ABC的形状是( )
| 3 |
| A、直角三角形 |
| B、等腰直角三角形 |
| C、钝角三角形 |
| D、正三角形 |