Question

已知点P（1，2），在直线l：x-y+4=0上求一点Q，使得|OQ|+|PQ|（O是坐标原点）最小，并求这个最小值．

Answer 1

考点：两点间距离公式的应用

专题：直线与圆

分析：如图所示，作点P关于直线l的对称点M，连接OM交直线l于点Q，则Q满足：使得|OQ|+|PQ|（O是坐标原点）最小．设M（a，b），则

a+1 2 - y+2 2 +4=0 b-2 a-1 ×1=-1

，解出即可．

解答： 解：如图所示，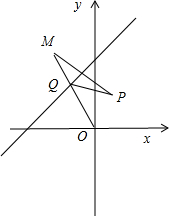
作点P关于直线l的对称点M，连接OM交直线l于点Q，则Q满足：使得|OQ|+|PQ|（O是坐标原点）最小．
设M（a，b），则

a+1 2 - y+2 2 +4=0 b-2 a-1 ×1=-1

，解得

a=-2 b=5

，
∴M（-2，5），可得直线OM的方程：y=-

5

2

x，
联立

5x+2y=0 x-y+4=0

，解得

x=- 8 7 y= 20 7

，
∴Q(-

8

7

，

20

7

)．
|OQ|+|PQ|最小值为|OM|=

(-2)2+52

=

29

．

点评：本题考查了对称点的求法、两点之间的距离根式，考查了推理能力与计算能力，属于中档题．