题目内容
直线4x+3y+19=0被圆x2+y2+4x+4y=0所截得的弦长为（ ）
| A、1 | ||
B、
| ||
| C、4 | ||
D、2
|
考点：直线与圆相交的性质
专题：直线与圆
分析：圆x2+y2+4x+4y=0的圆心C（-2，-2），半径r=
=2
，圆心C（-2，-2）到直线4x+3y+19=0的距离d=
=1，由此能求出直线4x+3y+19=0被圆x2+y2+4x+4y=0所截得的弦长．
| 1 |
| 2 |
| 16+16 |
| 2 |
| |4×(-2)+3×(-2)+19| | ||
|
解答：
解：圆x2+y2+4x+4y=0的圆心C（-2，-2），
半径r=
=2
，
圆心C（-2，-2）到直线4x+3y+19=0的距离：
d=
=1，
∴直线4x+3y+19=0被圆x2+y2+4x+4y=0所截得的弦长为：
|AB|=2
=2
=2
．
故选：D．
半径r=
| 1 |
| 2 |
| 16+16 |
| 2 |
圆心C（-2，-2）到直线4x+3y+19=0的距离：
d=
| |4×(-2)+3×(-2)+19| | ||
|
∴直线4x+3y+19=0被圆x2+y2+4x+4y=0所截得的弦长为：
|AB|=2
| r2-d2 |
| 8-1 |
| 7 |
故选：D．
点评：本题考查直线被圆截得的弦长的求法，是基础题，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
种植某种树苗，成活率为0.9，现采用随机模拟的方法估计该树苗种植5棵恰好4棵成活的概率，先由计算机产生0到9之间取整数值的随机数，指定1至9的数字代表成活，0代表不成活，再以每5个随机数为一组代表5次种植的结果．经随机模拟产生如下30组随机数：
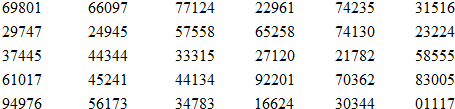
据此估计，该树苗种植5棵恰好4棵成活的概率为（ ）
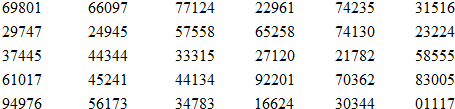
据此估计，该树苗种植5棵恰好4棵成活的概率为（ ）
| A、0.30 | B、0.35 |
| C、0.40 | D、0.50 |
两直线mx-2y+3=0与2x+2y-1=0互相垂直，则实数m的值为（ ）
| A、±2 | B、2 | C、-2 | D、0 |
设集合A={x|
≥0}，B=[0，1]，那么“m∈A”是“m∈B”的（ ）
| x |
| 1-x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要 |