题目内容
已知实数x、y满足x2+y2=3(y≥0),m=
,b=2x+y.求证:
(1)
≤m≤
;
(2)-2
≤b≤
.
| y+1 |
| x+3 |
(1)
3-
| ||
| 6 |
3+
| ||
| 6 |
(2)-2
| 3 |
| 15 |
考点:不等式的基本性质
专题:不等式
分析:(1)由题意可知的m=
几何意义是:圆上的点与(-3,-1)连线的斜率,作出图形,求出直线的斜率即可.
(2))b可看做斜率为-2过在圆x2+y2=3(y≥0)上点P(x,y)的直线在y轴上的截距,求出截距即可
| y+1 |
| x+3 |
(2))b可看做斜率为-2过在圆x2+y2=3(y≥0)上点P(x,y)的直线在y轴上的截距,求出截距即可
解答:
解:(1)由题意可知的m=
几何意义是:圆上的点与(-3,-1)连线的斜率,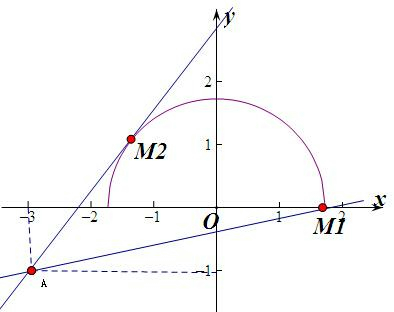
作出图形,可知k1≤m≤k2.(k1,k2分别为直线AM1,AM2的斜率),
k1=
=
,
圆心到切线k2x-y+3k2-1=0的距离为d=
=
,
解得k2=
(负值舍去),
故所求m的范围是:
≤m≤
.
问题得以证明.
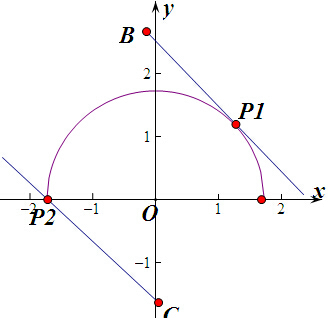
(2)b可看做斜率为-2过在圆x2+y2=3(y≥0)上点P(x,y)的直线在y轴上的截距,由图可知n2≤b≤n1,P2C的方程为y=-2(x+
)令x=0,
y=n2=-2
,
因为圆心到切线P1B:2x+y+c=0的距离为d=
=
,
解得c=±
,n1=
,
∴-2
≤b≤
| y+1 |
| x+3 |

作出图形,可知k1≤m≤k2.(k1,k2分别为直线AM1,AM2的斜率),
k1=
| 1 | ||
3+
|
3-
| ||
| 6 |
圆心到切线k2x-y+3k2-1=0的距离为d=
| |3k2-1| | ||
|
| 3 |
解得k2=
3±
| ||
| 6 |
故所求m的范围是:
3-
| ||
| 6 |
3+
| ||
| 6 |
问题得以证明.
(2)b可看做斜率为-2过在圆x2+y2=3(y≥0)上点P(x,y)的直线在y轴上的截距,由图可知n2≤b≤n1,P2C的方程为y=-2(x+
| 3 |
y=n2=-2
| 3 |
因为圆心到切线P1B:2x+y+c=0的距离为d=
| |c| | ||
|
| 3 |
解得c=±
| 15 |
| 15 |
∴-2
| 3 |
| 15 |

点评:本题是中档题,考查圆的方程与直线的斜率的关系,考查数形结合,注意圆的方程的范围,考查计算能力.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
执行如图所示的程序框图,若输出k=2,则输入x的取值范围是( )


| A、(28,57] |
| B、[28,57) |
| C、(28,57) |
| D、[28,57] |
 如图,△ABC的AB边长为2,P,Q分别是AC,BC中点,记
如图,△ABC的AB边长为2,P,Q分别是AC,BC中点,记| AB |
| AP |
| BA |
| BQ |
| AB |
| AQ |
| BA |
| BP |
| A、m=2,n=4 |
| B、m=3,n=1 |
| C、m=2,n=6 |
| D、m=3n,但m,n的值不确定 |