题目内容
20.非零向量$\overrightarrow{m}$,$\overrightarrow{n}$的夹角为$\frac{π}{3}$,且满足|$\overrightarrow{n}$|=λ|$\overrightarrow{m}$|(λ>0),向量组$\overrightarrow{{x}_{1}}$,$\overrightarrow{{x}_{2}}$,$\overrightarrow{{x}_{3}}$由一个$\overrightarrow{m}$和两个$\overrightarrow{n}$排列而成,向量组$\overrightarrow{{y}_{1}}$,$\overrightarrow{{y}_{2}}$,$\overrightarrow{{y}_{3}}$由两个$\overrightarrow{m}$和一个$\overrightarrow{n}$排列而成,若$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$所有可能值中的最小值为4$\overrightarrow{m}$2,则λ=$\frac{8}{3}$.分析 列出向量组的所有排列,计算所有可能的值,根据最小值列出不等式组解出.
解答 解:$\overrightarrow{m}•\overrightarrow{n}$=|$\overrightarrow{m}$|×λ|$\overrightarrow{m}$|×cos$\frac{π}{3}$=$\frac{λ}{2}$$\overrightarrow{m}$2,${\overrightarrow{n}}^{2}$=λ2$\overrightarrow{m}$2,
向量组$\overrightarrow{{x}_{1}}$,$\overrightarrow{{x}_{2}}$,$\overrightarrow{{x}_{3}}$共有3种情况,即($\overrightarrow{m}$,$\overrightarrow{n}$,$\overrightarrow{n}$),($\overrightarrow{n},\overrightarrow{m},\overrightarrow{n}$),($\overrightarrow{n},\overrightarrow{n},\overrightarrow{m}$),
向量组$\overrightarrow{{y}_{1}}$,$\overrightarrow{{y}_{2}}$,$\overrightarrow{{y}_{3}}$共有3种情况,即($\overrightarrow{m},\overrightarrow{m},\overrightarrow{n}$),($\overrightarrow{m},\overrightarrow{n},\overrightarrow{m}$),($\overrightarrow{n}$,$\overrightarrow{m},\overrightarrow{m}$),
∴$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$所有可能值有2种情况,即${\overrightarrow{m}}^{2}$+${\overrightarrow{n}}^{2}$+$\overrightarrow{m}•\overrightarrow{n}$=(λ2+λ+1)${\overrightarrow{m}}^{2}$,3$\overrightarrow{m}•\overrightarrow{n}$=$\frac{3λ}{2}$${\overrightarrow{m}}^{2}$,
∵$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$所有可能值中的最小值为4$\overrightarrow{m}$2,
∴$\left\{\begin{array}{l}{{λ}^{2}+λ+1≤\frac{3λ}{2}}\\{{λ}^{2}+λ+1=4}\end{array}\right.$或$\left\{\begin{array}{l}{{λ}^{2}+λ+1≥\frac{3λ}{2}}\\{\frac{3λ}{2}=4}\end{array}\right.$.
解得λ=$\frac{8}{3}$.
故答案为$\frac{8}{3}$.
点评 本题考查了平面向量的数量积运算,属于中档题.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | [$\frac{1}{5}$,1] | B. | [1,5] | C. | [$\frac{1}{5}$,5] | D. | (-∞,$\frac{1}{5}$]∪[5,+∞) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
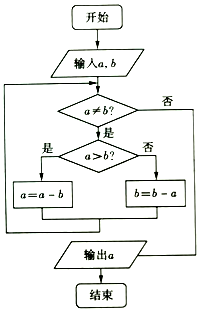 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )
如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )