题目内容
10.△ABC中,D是BC上的点,DA=DB=2,DC=1,则AB•AC的最大值是$\frac{9\sqrt{2}}{2}$.分析 由题意,D是BC上的点,DA=DB=2,DC=1,设AB=m,AC=n,根据余弦定理建立关系,利用基本不等式的性质求解.
解答 解:△ABC中,D是BC上的点,DA=DB=2,DC=1,设AB=m,AC=n,
cos∠BDA=$\frac{8-{m}^{2}}{8}$,cos∠CDA=$\frac{5-{n}^{2}}{4}$,
∠BDA与∠CDA互补,
∴$\frac{8-{m}^{2}}{8}$=-$\frac{5-{n}^{2}}{4}$,
可得:2n2+m2=18.
那么:AB•AC=m•n=$\frac{1}{\sqrt{2}}m•\sqrt{2}n$≤$\frac{1}{\sqrt{2}}$×$\frac{2{n}^{2}+{m}^{2}}{2}$=$\frac{9\sqrt{2}}{2}$(当且仅当m=$\sqrt{2}n$取等号)
故答案为$\frac{9\sqrt{2}}{2}$.
点评 本题考查了余弦定理的综合运用和基本不等式的性质的求解最值的问题.属于中档题.

练习册系列答案
相关题目
1.已知点O为△ABC的外心,且$|{\overrightarrow{BA}}|=2,|{\overrightarrow{BC}}|=6$,则$\overrightarrow{BO}•\overrightarrow{AC}$=( )
| A. | -32 | B. | -16 | C. | 32 | D. | 16 |
18. 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
(Ⅰ)求a,b,c的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(Ⅲ)某评估机构以指标M(M=$\frac{E(ξ)}{D(ξ)}$,其中D(ξ)表示ξ的方差)来评估该校安全教育活动的成效.若M≥0.7,则认定教育活动是有效的;否则认定教育活动五校,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(Ⅲ)某评估机构以指标M(M=$\frac{E(ξ)}{D(ξ)}$,其中D(ξ)表示ξ的方差)来评估该校安全教育活动的成效.若M≥0.7,则认定教育活动是有效的;否则认定教育活动五校,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
5.双曲线的焦点到渐近线的距离等于半实轴长,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
2.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P为双曲线C右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{10}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
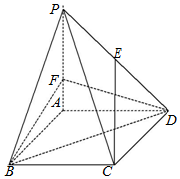 如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.