题目内容
过点P（a，5）作圆（x+2）2+（y-1）2=4的切线，切线长为2
，则a等于（ ）
| 3 |
| A、-1 | B、-2 | C、-3 | D、0 |
考点：圆的切线方程
专题：直线与圆
分析：算出圆心为C（-2，1）、半径r=2，根据两点间的距离公式，算出圆心到点P的距离|CP|．再由切线的性质利用勾股定理加以计算，可得a的值．
解答：
解：∵（x+2）2+（y-1）2=4的圆心为C（-2，1）、半径r=2，
∴点P（a，5）到圆心的距离为|CP|=
=
．
∵过切点的半径与切线垂直，
∴根据勾股定理，得切线长为2
=
．
解得：a=-2
故选：B．
∴点P（a，5）到圆心的距离为|CP|=
| (a+2)2+(5-1)2 |
| (a+2)2+16 |
∵过切点的半径与切线垂直，
∴根据勾股定理，得切线长为2
| 3 |
(
|
解得：a=-2
故选：B．
点评：本题考查求圆的经过点P的切线长．着重考查了圆的标准方程、两点间的距离公式、切线的性质与勾股定理等知识，属于中档题．
练习册系列答案
相关题目
下列向量运算中，结果为
的是（ ）
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知2cosα=sinα，则
的值为（ ）
| sin2α |
| cos2α |
A、
| ||
| B、2 | ||
| C、4 | ||
| D、8 |
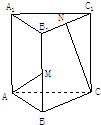如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，M、N分别是BB1和B1C1的中点，则直线AM与CN所成角的余弦值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列8，5，2，…的第20项是（ ）
| A、68 | B、65 |
| C、-46 | D、-49 |