题目内容
下列向量运算中，结果为
的是（ ）
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：向量的三角形法则
专题：平面向量及应用
分析：由向量的三角形法则，逐个选项验证可得．
解答：
解：由向量的运算法则可得选项B，
+
=
，故正确；
而选项A和C所得向量均和
无直接关系；
选项D，
-
=
，故错误．
故选：B
| AC |
| CB |
| AB |
而选项A和C所得向量均和
| AB |
选项D，
| OA |
| OB |
| BA |
故选：B
点评：本题考查向量的三角形法则，属基础题．
练习册系列答案
相关题目
已知i为虚数单位，则复平面内表示复数z=i（1-i）的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
由一组数据（x1，y1）、（x2，y2）、…、（xn，yn）得到的线性回归方程为y=a+bx，则下列说法正确的是（ ）
A、直线y=a+bx必过点（
| ||||
| B、直线y=a+bx至少经过点（x1，y1）、（x2，y2）、…、（xn，yn）中的一点 | ||||
| C、直线y=a+bx是由（x1，y1）、（x2，y2）、…、（xn，yn）中的两点确定的 | ||||
| D、（x1，y1）、（x2，y2）、…、（xn，yn），这n个点到直线y=a+bx的距离之和最小 |
设集合A={x|x+1≥0}，集合B=|x|x≥0}，则A∪B=（ ）
| A、∅ |
| B、[0，+∞） |
| C、[-1，+∞） |
| D、[1，+∞） |
已知f（x）=ax3+bx2+cx是定义在[a-1，2a]上的奇函数，则a+b=（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|
用反证法证明命题“设x，y∈（0，1），求证：对于a，b∈R，必存在满足条件的x，y，使|xy-ax-by|≥
成立．”第一步的假设为（ ）
| 1 |
| 3 |
A、对任意x，y∈（0，1），|xy-ax-by|≥
| ||
B、对任意x，y∈（0，1），|xy-ax-by|＜
| ||
C、存在x，y∈（0，1），使|xy-ax-by|＜
| ||
D、存在x，y∉（0，1），使|xy-ax-by|≥
|
过点P（a，5）作圆（x+2）2+（y-1）2=4的切线，切线长为2
，则a等于（ ）
| 3 |
| A、-1 | B、-2 | C、-3 | D、0 |
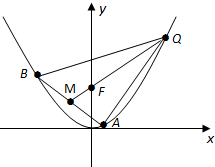已知抛物线C：x2=2py，的焦点为F，△ABQ的三个顶点都在抛物线C上，点M为AB的中点，