题目内容
设函数f(x)=ax2+bx+c,且f(1)=-
,3a>2c>2b,求证:
(1)a>0且-3<
<-
;
(2)函数f(x)在区间(0,2)内至少有一个零点.
| a |
| 2 |
(1)a>0且-3<
| b |
| a |
| 3 |
| 4 |
(2)函数f(x)在区间(0,2)内至少有一个零点.
考点:二次函数的性质
专题:证明题,函数的性质及应用
分析:(1)由f(1)=-
,推出3a+2b+2c=0,再由3a>2c>2b,即可得到a>0,b<0,再将2c=-3a-2b代入3a>2c>2b,应用不等式的性质,即可得证;
(2)求出f(0),f(2),讨论c>0,f(0),f(1)的符号,以及c≤0,f(1),f(2)的符号,应用零点存在定理,即可得证.
| a |
| 2 |
(2)求出f(0),f(2),讨论c>0,f(0),f(1)的符号,以及c≤0,f(1),f(2)的符号,应用零点存在定理,即可得证.
解答:
证明:(1)∵f(1)=a+b+c=-
,∴3a+2b+2c=0,
又3a>2c>2b,∴3a>0,2b<0,∴a>0,b<0,
又2c=-3a-2b 由3a>2c>2b∴3a>-3a-2b>2b,
∵a>0,∴-3<
<-
;
(2)∵f(0)=c,f(2)=4a+2b+c=a-c,
①当c>0时,∵a>0,∴f(0)=c>0且f(1)=-
<0,
∴函数f(x)在区间(0,1)内至少有一个零点;
②当c≤0时,∵a>0∴且f(1)=-
<0,且f(2)=a-c>0,
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点.
| a |
| 2 |
又3a>2c>2b,∴3a>0,2b<0,∴a>0,b<0,
又2c=-3a-2b 由3a>2c>2b∴3a>-3a-2b>2b,
∵a>0,∴-3<
| b |
| a |
| 3 |
| 4 |
(2)∵f(0)=c,f(2)=4a+2b+c=a-c,
①当c>0时,∵a>0,∴f(0)=c>0且f(1)=-
| a |
| 2 |
∴函数f(x)在区间(0,1)内至少有一个零点;
②当c≤0时,∵a>0∴且f(1)=-
| a |
| 2 |
∴函数f(x)在区间(1,2)内至少有一个零点.
综合①②得f(x)在(0,2)内至少有一个零点.
点评:本题主要考查二次函数的性质,考查函数的零点存在定理及应用,考查逻辑推理能力,是一道综合题.

练习册系列答案
相关题目
过点P(a,5)作圆(x+2)2+(y-1)2=4的切线,切线长为2
,则a等于( )
| 3 |
| A、-1 | B、-2 | C、-3 | D、0 |
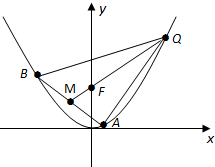 已知抛物线C:x2=2py,的焦点为F,△ABQ的三个顶点都在抛物线C上,点M为AB的中点,
已知抛物线C:x2=2py,的焦点为F,△ABQ的三个顶点都在抛物线C上,点M为AB的中点,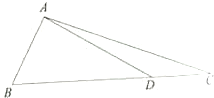 如图,△ABC中,D在边BC上,BD=2,CD=1,AD=
如图,△ABC中,D在边BC上,BD=2,CD=1,AD=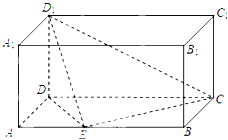 在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.